Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải bài 26 trang 62 sách bài tập Toán 8 Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
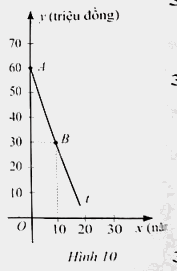
Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng
Đề bài
Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng, mỗi năm thiết bị tiệt khuẩn đó đều khấu hao \(k\) (triệu đồng) với \(0 < k < 60\). Gọi \(y\) (triệu đồng) là giá của thiết bị tiệt khuẩn đó sau \(x\) năm sử dụng.
a) Chứng tỏ rẳng \(y\) là hàm số bậc nhất của \(x\), tức là \(y = ax + b\left( {a \ne 0} \right)\).
b) Trong Hình 10, tia \(At\) là một phần của đường thẳng \(y = ax + b\). Tìm \(a,b\). Từ đó, cho biết sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng bao nhiêu phần trăm so với giá mua ban đầu.
Phương pháp giải - Xem chi tiết
Dựa vào đồ thi của hàm số bậc nhất để tính tỉ số phần trăm giữa giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng và giá mua ban đầu.
Lời giải chi tiết
a) Công thức biểu thị giá của thiết bị tiệt khuẩn đó sau \(x\) năm sử dụng là: \(y = 60 - kx\) hay \(y = - kx + 60\). Mà \(k \ne 0\), suy ra \(y\) là hàm số bậc nhất của \(x\).
b) Từ câu a, ta có \(b = 60\). Do đường thẳng \(y = ax + b\) đi qua điểm \(B\left( {10;30} \right)\) nên \(30 = a.10 + 60\). Suy ra \(a = - 3\). Khi đó, đường thẳng cần tìm là: \(y = - 3x + 60\).
Giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng là:
\( - 3.12 + 60 = 24\) (triệu đồng)
Tỉ số phần trăm giữa giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng và giá mua ban đầu là: \(\frac{{24.100}}{{60}}\% = 40\% \).
Vậy sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng \(40\% \) so với giá mua ban đầu.
Bài 26 trang 62 sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc ôn tập và củng cố kiến thức về các dạng bài tập liên quan đến hình học, cụ thể là các tính chất của hình thang cân. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 26 trang 62 sách bài tập Toán 8 Cánh Diều thường bao gồm các dạng bài tập sau:
Để giải bài 26 trang 62 sách bài tập Toán 8 Cánh Diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Bài toán: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = BC = 6cm. Tính chiều cao của hình thang.
Giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Khi đó, AH = BK = h (chiều cao của hình thang).
Ta có: DH = KC = (CD - AB)/2 = (10 - 5)/2 = 2.5cm.
Áp dụng định lý Pitago vào tam giác vuông ADH, ta có:
AD2 = AH2 + DH2
62 = h2 + 2.52
h2 = 36 - 6.25 = 29.75
h = √29.75 ≈ 5.45cm
Vậy chiều cao của hình thang là khoảng 5.45cm.
Khi giải bài tập về hình thang cân, bạn cần chú ý những điều sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về hình thang cân, bạn có thể tham khảo các bài tập sau:
Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể giải bài 26 trang 62 sách bài tập Toán 8 Cánh Diều một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!