Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 16 trang 65 Sách bài tập Toán 8 – Cánh Diều. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải cụ thể, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Cho tam giác \(ABC\) cân tại \(A\), có \(M\) là trung điểm của \(BC\). Kể tia \(Mx\) song song với \(AC\) cắt \(AB\) tại \(E\) và tia \(My\) song song với \(AB\) cắt \(AC\) tại \(F\). Chứng minh:
Đề bài
Cho tam giác \(ABC\) cân tại \(A\), có \(M\) là trung điểm của \(BC\). Kể tia \(Mx\) song song với \(AC\) cắt \(AB\) tại \(E\) và tia \(My\) song song với \(AB\) cắt \(AC\) tại \(F\). Chứng minh:
a) \(EF\) là đường trung bình của tam giác \(ABC\);
b) \(AM\) là đường trung trực của \(EF\).
Phương pháp giải - Xem chi tiết
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh tam giác đó.
Tính chất: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó.
Lời giải chi tiết
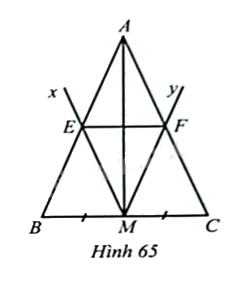
a) Vì \(M\) là trung điểm của \(BC,ME//AC,MF//AB\) nên \(E,F\) lần lượt là trung điểm của \(AB.AC\). Do đó, \(EF\) là đường trung bình của tam giác \(ABC\).
b) Ta có \(AE = \frac{{AB}}{2},AF = \frac{{AC}}{2}\) và \(AB = AC\) suy ra \(AE = AF\) (1). Lại có \(ME,MF\) là các đường trung bình của tam giác \(ABC\) nên \(ME = \frac{{AC}}{2},MF = \frac{{AB}}{2}\). Mà \(AB = AC\) suy ra \(ME = MF\) (2). Từ (1) và (2) suy ra \(AM\) là đường trung trực của \(EF\).
Bài 16 trang 65 Sách bài tập Toán 8 – Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập yêu cầu học sinh chứng minh các tính chất, tính toán độ dài đoạn thẳng và giải quyết các bài toán thực tế liên quan đến hình thang cân.
Bài 16 bao gồm các câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Hình thang cân là hình thang có hai cạnh bên song song. Các tính chất của hình thang cân bao gồm:
Vì AB // CD nên:
Gọi tứ giác đó là ABCD (AB // CD) và góc A = góc B. Ta cần chứng minh AD = BC.
Kẻ đường cao AH và BK xuống CD. Khi đó, tam giác AHD và tam giác BKC bằng nhau (cạnh huyền – góc nhọn) do đó AD = BC. Vậy tứ giác ABCD là hình thang cân.
Để giải các bài tập về hình thang cân một cách hiệu quả, bạn nên:
Hình thang cân xuất hiện trong nhiều ứng dụng thực tế, ví dụ như:
Để củng cố kiến thức về hình thang cân, bạn có thể làm thêm các bài tập sau:
Bài 16 trang 65 Sách bài tập Toán 8 – Cánh Diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các tính chất và ứng dụng của hình thang cân. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập liên quan đến hình thang cân.