Bài 46 trang 78 sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các dạng toán hình học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 46 trang 78, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
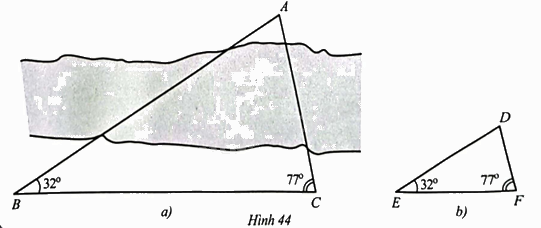
Bác An cần đo khoảng cách \(AC\), với \(A,C\) nằm ở hai bên bờ của một hồ nướ (Hình 44a). Bác An đã tiến hành đo như sau:
Đề bài
Bác An cần đo khoảng cách \(AC\), với \(A,C\) nằm ở hai bên bờ của một hồ nướ (Hình 44a). Bác An đã tiến hành đo như sau:
- Chọn điểm \(B\) trên bờ (có điểm \(C\)) sao cho \(BC = 20\) (m).
- Dùng thước đo góc, đo được các góc \(\widehat {ABC} = 32^\circ ,\widehat {ACB} = 77^\circ \).
Chứng minh rằng: Nếu thực hiện vẽ trên giấy một tam giác \(DEF\) sao cho \(EF = 10\) (cm), \(\widehat {DEF} = 32^\circ ,\widehat {DFE} = 77^\circ \) (Hình 44b); Đo độ dài đoạn \(DF\) và giả sử \(DF = a\) (cm) thì độ dài \(AC\) mà bác An cần đo là \(2a\) (m).
Phương pháp giải - Xem chi tiết
Áp dụng trường hợp đồng dạng thứ ba: góc – góc
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết
Ta có \(\Delta ABC\backsim \Delta DEF\) \( = > \frac{{BC}}{{EF}} = \frac{{AC}}{{DF}}\) hay \(\frac{{2000}}{{10}} = \frac{{AC}}{a}\)
Do đó \(AC = 200a\) (cm) \( = 2a\) (m).
Bài 46 trang 78 sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc ôn luyện và củng cố kiến thức về các dạng bài toán hình học đã được học. Bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất đã biết để chứng minh các mối quan hệ giữa các yếu tố hình học, tính toán diện tích, chu vi, hoặc giải các bài toán thực tế liên quan đến hình học.
Bài 46 thường bao gồm các dạng bài tập sau:
Để giải quyết bài tập 46 trang 78 một cách hiệu quả, học sinh cần:
(Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 46. Ví dụ:)
Câu a: Cho hình thang ABCD (AB // CD). Gọi M là trung điểm của AD, N là trung điểm của BC. Chứng minh rằng MN // AB // CD.
Lời giải:
Gọi E là giao điểm của AC và BD. Vì AB // CD nên ta có: ΔABE ~ ΔCDE (g.g). Suy ra AE/EC = BE/ED = AB/CD.
Xét ΔADE, M là trung điểm của AD nên EM là đường trung bình của ΔADE. Suy ra EM // DE.
Xét ΔBCD, N là trung điểm của BC nên EN là đường trung bình của ΔBCD. Suy ra EN // BD.
Vì EM // DE và EN // BD mà DE // BD nên EM // EN. Do đó, M, E, N thẳng hàng. Vậy MN // AB // CD.
Ngoài bài 46, học sinh có thể tham khảo các bài tập tương tự trong sách bài tập Toán 8 Cánh Diều và các tài liệu tham khảo khác để luyện tập và củng cố kiến thức. Một số tài liệu hữu ích bao gồm:
Để học tốt môn Toán 8, học sinh cần:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập 46 trang 78 sách bài tập Toán 8 Cánh Diều và đạt kết quả tốt trong môn Toán.