Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 8 sách Cánh Diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 20 trang 66, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 20 trang 66 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho tứ giác \(ABCD\) có \(M,N\) lần lượt là trung điểm của \(AD,BC\). Chứng minh: \(MN \le \frac{{AB + DC}}{2}\). Dấu đẳng thức xảy ra khi nào?
Đề bài
Cho tứ giác \(ABCD\) có \(M,N\) lần lượt là trung điểm của \(AD,BC\). Chứng minh: \(MN \le \frac{{AB + DC}}{2}\). Dấu đẳng thức xảy ra khi nào?
Phương pháp giải - Xem chi tiết
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh tam giác đó.
Tính chất: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó.
Lời giải chi tiết
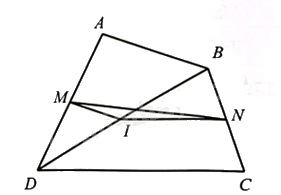
Lấy \(I\) là trung điểm của \(BD\). Khi đó, ta có \(MI,NI\) lần lượt là các đường trung bình của tam giác \(ABD\) và \(BDC\) nên \(MI = \frac{{AB}}{2},NI = \frac{{CD}}{2}\).
Do đó \(MI + NI = \frac{{AB + CD}}{2}\) (1)
- Nếu \(I\) không thuộc \(MN\) ta có \(MN < MI + NI\) (bất đẳng thức tam giác).
- Nếu \(I\) thuộc \(MN\) ta có \(MN = MI + NI\).
Tức là, ta luôn có \(MN \le MI + NI\) (2). Từ (1) và (2) suy ra \(MN \le \frac{{AB + CD}}{2}\).
Dấu đẳng thức xảy ra khi \(I\) thuộc \(MN\), khi đó \(AB//CD\).
Bài 20 trang 66 sách bài tập Toán 8 Cánh Diều thuộc chương trình học về các tứ giác đặc biệt. Để giải bài tập này, học sinh cần nắm vững các kiến thức về hình thang cân, hình bình hành, hình chữ nhật, hình vuông và các tính chất liên quan.
Bài tập 20 bao gồm các câu hỏi liên quan đến việc xác định loại tứ giác, tính độ dài cạnh, góc và ứng dụng các tính chất của các tứ giác đặc biệt để giải quyết các bài toán thực tế.
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi qua từng câu hỏi cụ thể:
Đề bài: Cho hình thang cân ABCD (AB // CD). Gọi M là trung điểm của AD, N là trung điểm của BC. Chứng minh rằng MN là đường trung bình của hình thang.
Lời giải:
Đề bài: Nếu AB = 5cm, CD = 10cm thì độ dài MN bằng bao nhiêu?
Lời giải:
Áp dụng công thức tính độ dài đường trung bình của hình thang, ta có:
MN = (AB + CD) / 2 = (5 + 10) / 2 = 7.5cm
Đề bài: Nếu góc A = 80° thì góc D bằng bao nhiêu?
Lời giải:
Vì ABCD là hình thang cân nên góc A = góc D và góc B = góc C. Do đó, góc D = 80°.
Ngoài bài tập 20, sách bài tập Toán 8 Cánh Diều còn có nhiều bài tập tương tự về các tứ giác đặc biệt. Để giải tốt các bài tập này, học sinh cần:
Bài tập: Cho hình bình hành ABCD. Gọi E là trung điểm của AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng AF = 2FC.
Lời giải:
Khi giải bài tập về tứ giác, học sinh cần chú ý:
Bài 20 trang 66 sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về các tứ giác đặc biệt. Hy vọng với hướng dẫn chi tiết và dễ hiểu trên đây, các bạn học sinh sẽ tự tin hơn trong quá trình học tập và giải bài tập Toán 8.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc các bạn học tốt!