Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 sách Cánh Diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 11 trang 62, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
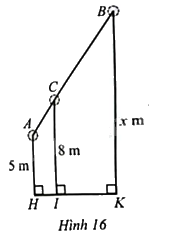
Ở một nhà máy, người ta dùng một băng chuyền để chuyển nguyên vật liệu. Ba vòng quay (A,B,C) của băng chuyền đặt cách mặt đất ở các độ cao lần lượt là (AH = 5) (m), (CI = 8) (m), (BK = x) (m) (Hình 16).
Đề bài
Ở một nhà máy, người ta dùng một băng chuyền để chuyển nguyên vật liệu. Ba vòng quay \(A,B,C\) của băng chuyền đặt cách mặt đất ở các độ cao lần lượt là \(AH = 5\) (m), \(CI = 8\) (m), \(BK = x\) (m) (Hình 16).
Tính \(x\), biết \(AC = \frac{2}{5}CB\)
Phương pháp giải - Xem chi tiết
Áp dụng định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
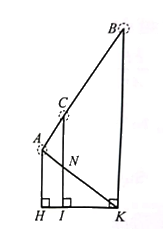
Do \(AC = \frac{2}{5}CB\) nên \(AC = \frac{2}{7}AB\). Gọi \(N\) là giao điểm của \(AK\) và \(CI\). Do \(CN//BK\) nên theo hệ quả của định lí Thales, ta có: \(\frac{{AC}}{{AB}} = \frac{{CN}}{{BK}}\) hay \(\frac{{CN}}{x} = \frac{2}{7}\). Suy ra \(CN = \frac{2}{7}x\) (1). Tương tự, do \(IN//AH,CN//BK\) nên \(\frac{{IN}}{{AH}} = \frac{{IK}}{{KH}} = \frac{{BK}}{{KA}} = \frac{{CB}}{{BA}} = \frac{5}{7}\) hay \(\frac{{IN}}{5} = \frac{5}{7}\). Suy ra \(IN = 5.\frac{5}{7} = \frac{{25}}{7}\) (m) (2).
Từ (1) và (2) ta có: \(CI = CN + IN = \frac{2}{7}x + \frac{{25}}{7}\).
Lại có \(CI = 8\) (m) nên \(\frac{2}{7}x + \frac{{25}}{7} = 8\). Vậy \(x = 15,5\).
Bài 11 trang 62 sách bài tập Toán 8 Cánh Diều thuộc chương trình học về hình hộp chữ nhật và hình lập phương. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi bắt tay vào giải bài tập, hãy đọc kỹ đề bài và xác định rõ yêu cầu. Thông thường, bài tập về hình học sẽ yêu cầu tính diện tích, thể tích hoặc xác định mối quan hệ giữa các yếu tố của hình. Để giải quyết bài toán, bạn có thể áp dụng các phương pháp sau:
Đề bài: (Giả sử đề bài là: Một hình hộp chữ nhật có chiều dài 8cm, chiều rộng 6cm và chiều cao 5cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật đó.)
Giải:
Diện tích xung quanh của hình hộp chữ nhật là: 2 * (chiều dài + chiều rộng) * chiều cao = 2 * (8 + 6) * 5 = 2 * 14 * 5 = 140 cm2
Diện tích toàn phần của hình hộp chữ nhật là: Diện tích xung quanh + 2 * (chiều dài * chiều rộng) = 140 + 2 * (8 * 6) = 140 + 2 * 48 = 140 + 96 = 236 cm2
Thể tích của hình hộp chữ nhật là: chiều dài * chiều rộng * chiều cao = 8 * 6 * 5 = 240 cm3
Ngoài bài 11 trang 62, sách bài tập Toán 8 Cánh Diều còn có nhiều bài tập tương tự về hình hộp chữ nhật và hình lập phương. Dưới đây là một số dạng bài tập thường gặp và cách giải:
Để học tốt môn Toán 8, đặc biệt là các bài tập về hình học, bạn có thể áp dụng một số mẹo sau:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 11 trang 62 sách bài tập Toán 8 Cánh Diều. Hãy luyện tập thường xuyên và áp dụng các mẹo học tập hiệu quả để đạt kết quả tốt nhất trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!