Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 36 trang 72 sách bài tập Toán 8 Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 36 trang 72 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
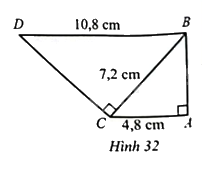
Quan sát Hình 32 có (widehat {BAC} = 90^circ ,widehat {BCD} = 90^circ ,DB = 10,8)cm, (BC = 7,2)cm và (CA = 4,8)cm. Chứng minh: (Delta DBCbacksim Delta BCA).
Đề bài
Quan sát Hình 32 có \(\widehat {BAC} = 90^\circ ,\widehat {BCD} = 90^\circ ,DB = 10,8\)cm, \(BC = 7,2\)cm và \(CA = 4,8\)cm. Chứng minh: \(\Delta DBC\backsim \Delta BCA\).
Phương pháp giải - Xem chi tiết
Áp dụng trường hợp đồng dạng thứ nhất của tam giác vào tam giác vuông:
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải chi tiết
Nhận thấy: \(\frac{{DB}}{{CB}} = \frac{{10,8}}{{7,2}} = \frac{3}{2},\frac{{BC}}{{CA}} = \frac{{7,2}}{{4,8}} = \frac{3}{2}\). Từ đó ta có: tam giác \(DBC\) vuông tại đỉnh \(C\), tam giác \(BCA\) vuông tại đỉnh \(A\) và \(\frac{{DB}}{{CB}} = \frac{{BC}}{{CA}}\) (vì cùng bằng \(\frac{3}{2}\)). Suy ra \(\Delta DBC\backsim \Delta BCA\).
Bài 36 trang 72 sách bài tập Toán 8 Cánh Diều thuộc chương trình học về hình học, cụ thể là phần kiến thức liên quan đến tứ giác. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về tứ giác, các tính chất của tứ giác đặc biệt (hình chữ nhật, hình thoi, hình vuông, hình bình hành) và các định lý liên quan đến tứ giác.
Bài 36 thường xoay quanh việc chứng minh một tứ giác là một hình đặc biệt nào đó dựa trên các điều kiện cho trước. Các điều kiện này có thể là về độ dài cạnh, góc, đường chéo hoặc mối quan hệ giữa chúng. Để giải bài toán, học sinh cần phân tích kỹ đề bài, xác định các yếu tố đã cho và lựa chọn phương pháp chứng minh phù hợp.
Có nhiều phương pháp khác nhau để chứng minh một tứ giác là một hình đặc biệt. Một số phương pháp phổ biến bao gồm:
Đề bài: Cho tứ giác ABCD có AB = CD và AD = BC. Chứng minh rằng tứ giác ABCD là hình bình hành.
Lời giải:
Khi giải bài toán về tứ giác, học sinh cần chú ý:
Để củng cố kiến thức và kỹ năng giải bài toán về tứ giác, học sinh nên làm thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn trong các bài kiểm tra.
Bài 36 trang 72 sách bài tập Toán 8 Cánh Diều là một bài toán quan trọng giúp học sinh hiểu sâu hơn về các khái niệm và tính chất của tứ giác. Hy vọng rằng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các bạn học sinh sẽ giải quyết bài toán một cách dễ dàng và hiệu quả.