Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải bài 14 trang 77 sách bài tập Toán 8 Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
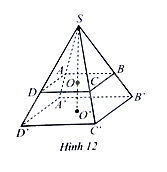
Cho hai hình chóp tứ giác đều \(S.ABCD\) và \(S.A'B'C'D'\) lần lượt có chiều cao \(SO\) và \(SO'\). Biết \(AB = 2a,A'B' = 3a,SO = 2b,SO' = 3b\) (Hình 12).
Đề bài
Cho hai hình chóp tứ giác đều \(S.ABCD\) và \(S.A'B'C'D'\) lần lượt có chiều cao \(SO\) và \(SO'\). Biết \(AB = 2a,A'B' = 3a,SO = 2b,SO' = 3b\) (Hình 12). Tính tỉ số thể tích của hình chóp tứ giác đều \(S.ABCD\) và \(S.A'B'C'D'\) biết rẳng \(a\) và \(b\) cùng đơn vị đo.
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính thể tích của hình chóp tứ giác đều: \(V = \frac{1}{3}.S.h\), trong đó \(V\) là thể tích, \(S\) là diện tích đáy, \(h\) là chiều cao của hình chóp tứ giác đều. Sau đó tính tỉ số thể tích của hai hình chóp tứ giác đều đó.
Lời giải chi tiết
Thể tích của hình chóp tứ giác đều \(S.ABCD\) là:
\(\frac{1}{3}.\left( {2a.2a} \right).2b = \frac{{8{a^2}b}}{3}\) (đơn vị thể tích)
Thể tích của hình chóp tứ giác đều \(S.A'B'C'D'\) là:
\(\frac{1}{3}.\left( {3a.3a} \right).3b = 9{a^2}b\) (đơn vị thể tích)
Tỉ số thể tích của hình chóp tứ giác đều \(S.ABCD\) và \(S.A'B'C'D'\) là:
\(\frac{{8{a^2}b}}{3}:\left( {9{a^2}b} \right) = \frac{8}{{27}}\)
Bài 14 trang 77 sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Bài 14 trang 77 thường yêu cầu học sinh chứng minh một hình thang cân hoặc tính toán các yếu tố của hình thang cân dựa trên các dữ kiện đã cho. Để giải bài toán này, bạn có thể áp dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết cho từng phần của bài 14, bao gồm các bước giải, giải thích và kết luận. Ví dụ:)
a) Chứng minh tứ giác ABCD là hình thang cân:
Ta có: AB // CD (giả thiết). Do đó, tứ giác ABCD là hình thang.
Xét tam giác ABD và tam giác CDB, ta có:
Do đó, tam giác ABD = tam giác CDB (c-g-c). Suy ra AD = BC.
Vậy, tứ giác ABCD là hình thang cân.
b) Tính độ dài các cạnh AD và BC:
Vì ABCD là hình thang cân nên AD = BC. Theo đề bài, AB = 5cm, CD = 10cm. Để tính AD và BC, ta cần thêm thông tin về chiều cao hoặc góc của hình thang.
Ngoài bài 14 trang 77, còn rất nhiều bài tập tương tự về hình thang cân trong sách bài tập Toán 8 Cánh Diều. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để củng cố kiến thức về hình thang cân và rèn luyện kỹ năng giải toán, bạn nên làm thêm các bài tập trong sách bài tập Toán 8 Cánh Diều và các tài liệu tham khảo khác. Bạn cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học Toán 8 để được hướng dẫn chi tiết hơn.
Bài 14 trang 77 sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hình thang cân và các tính chất của nó. Bằng cách nắm vững lý thuyết, phân tích bài toán một cách cẩn thận và vận dụng các phương pháp giải phù hợp, bạn có thể giải quyết bài toán này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!