Giải bài 32 trang 102 Sách bài tập Toán 8 Cánh Diều

Giải bài 32 trang 102 sách bài tập toán 8 - Cánh diều

Giải bài 32 trang 102 Sách bài tập Toán 8 Cánh Diều

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 sách Cánh Diều. Bài viết này sẽ hướng dẫn bạn giải bài 32 trang 102 một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải toán.

Cho hình chữ nhật \(ABCD\) có hai cạnh kề không bằng nhau. Tia phân giác của các góc \(A\) và \(B\) cắt nhau tại \(E\).

Đề bài

Cho hình chữ nhật \(ABCD\) có hai cạnh kề không bằng nhau. Tia phân giác của các góc \(A\) và \(B\) cắt nhau tại \(E\). Tia phân giác của các góc \(C\) và \(D\) cắt nhau tại \(F\). Gọi \(G\) là giao điểm của \(AE\) và \(DF\), \(H\) là giao điểm của \(BE\) và \(CF\). Chứng minh:

a) \(GH//CD\)

b) Tứ giác \(GFHE\) là hình vuông

Phương pháp giải - Xem chi tiết Giải bài 32 trang 102 sách bài tập toán 8 - Cánh diều 1

Dựa vào dấu hiệu nhận biết của hình vuông:

- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông

- Hình chữ nhật có hai đường chéo là đường phân giác của một góc là hình vuông

Lời giải chi tiết

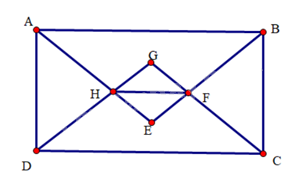
Giải bài 32 trang 102 sách bài tập toán 8 - Cánh diều 2

a) Do \(ABCD\) là hình chữ nhật nên \(\widehat {DAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDA} = 90^\circ \)

Mà \(AE,BE,CF,DF\) lần lượt là các tia phân giác của các góc \(DAB,ABC,BCD,CDA\) suy ra \(\widehat {DAE} = \widehat {EAB} = \widehat {ABE} = \widehat {EBC} = \widehat {BCF} = \widehat {FCD} = \widehat {CDF} = \widehat {FDA} = 45^\circ \)

Do đó, các tam giác \(EAB,FCD,GAD,HBC\) đều là tam giác vuông cân.

\(\Delta GAD = \Delta HBC\) (g.c.g). Suy ra \(GD = HC\). Mà \(FD = FC\), suy ra \(FG = FH\).

Do đó, tam giác \(FGH\) vuông cân tại \(F\). Suy ra \(\widehat {FGH} = 45^\circ \).

Ta có: \(\widehat {FGH} = \widehat {CDF} = 45^\circ \) và \(\widehat {FGH},\widehat {CDF}\) nằm ở vị trí đồng vị nên \(GH//CD\).

b) \(\widehat {EGF} = \widehat {AGD} = 90^\circ \) (hai góc đối đỉnh)

Tứ giác \(GFHE\) là hình chữ nhật.

Hình chữ nhật \(GFHE\) có \(FG = FH\) nên \(GFHE\) là hình vuông.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 32 trang 102 sách bài tập toán 8 - Cánh diều đặc sắc thuộc chuyên mục toán 8 sgk trên môn toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 32 trang 102 Sách bài tập Toán 8 Cánh Diều: Tổng quan

Bài 32 trang 102 sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc ôn tập và củng cố kiến thức về các dạng bài tập liên quan đến hình học, cụ thể là các tính chất của hình thang cân. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và khả năng giải quyết vấn đề.

Nội dung chi tiết bài 32 trang 102

Bài 32 bao gồm các câu hỏi và bài tập khác nhau, yêu cầu học sinh:

Nhận biết các yếu tố của hình thang cân (đáy lớn, đáy nhỏ, cạnh bên, đường cao).
Vận dụng các tính chất của hình thang cân để chứng minh các tính chất hình học.
Tính toán các yếu tố của hình thang cân (độ dài cạnh, đường cao, diện tích).
Giải các bài toán thực tế liên quan đến hình thang cân.

Hướng dẫn giải chi tiết bài 32 trang 102

Câu 1: (SBT Toán 8 Cánh Diều, trang 102)

Đề bài: Cho hình thang cân ABCD (AB // CD). Gọi M là trung điểm của AD, N là trung điểm của BC. Chứng minh rằng MN là đường trung bình của hình thang.

Lời giải:

Gọi I là giao điểm của AC và MN.
Chứng minh tam giác ADI đồng dạng với tam giác MCI (cạnh góc vuông - cạnh góc vuông).
Suy ra AI = IC.
Tương tự, gọi J là giao điểm của BD và MN. Chứng minh BJ = JD.
Suy ra MN là đường trung bình của hình thang ABCD.

Câu 2: (SBT Toán 8 Cánh Diều, trang 102)

Đề bài: Cho hình thang cân ABCD (AB // CD). Biết AB = 5cm, CD = 10cm, AD = 6cm. Tính độ dài đường cao của hình thang.

Lời giải:

Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Khi đó, AH = BK là đường cao của hình thang.

Ta có: DH = KC = (CD - AB) / 2 = (10 - 5) / 2 = 2.5cm.

Áp dụng định lý Pitago vào tam giác ADH vuông tại H, ta có:

AH² = AD² - DH² = 6² - 2.5² = 36 - 6.25 = 29.75

Suy ra: AH = √29.75 ≈ 5.45cm.

Vậy, độ dài đường cao của hình thang là khoảng 5.45cm.

Câu 3: (SBT Toán 8 Cánh Diều, trang 102)

Đề bài: Cho hình thang cân ABCD (AB // CD). Biết góc A = 70^o. Tính các góc còn lại của hình thang.

Lời giải:

Vì ABCD là hình thang cân nên góc A = góc B = 70^o.

Mặt khác, góc A + góc D = 180^o (hai góc kề trong cùng phía).

Suy ra: góc D = 180^o - 70^o = 110^o.

Tương tự, góc C = góc D = 110^o.

Vậy, các góc còn lại của hình thang là: góc B = 70^o, góc C = 110^o, góc D = 110^o.

Mẹo giải bài tập hình thang cân

Nắm vững các tính chất của hình thang cân: hai cạnh bên bằng nhau, hai đường chéo bằng nhau, hai góc kề một đáy bằng nhau.
Sử dụng các định lý và hệ quả của định lý Pitago để tính toán các yếu tố của hình thang cân.
Vẽ hình chính xác và chú thích các yếu tố đã biết để dễ dàng hình dung và giải quyết bài toán.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải toán.

Kết luận

Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 32 trang 102 sách bài tập Toán 8 Cánh Diều. Hãy luyện tập thêm các bài tập tương tự để củng cố kiến thức và nâng cao kỹ năng giải toán của mình. Chúc bạn học tập tốt!