Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 8 trang 34 sách bài tập Toán 8 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic, kèm theo các ví dụ minh họa để bạn dễ dàng tiếp thu và áp dụng vào thực tế.
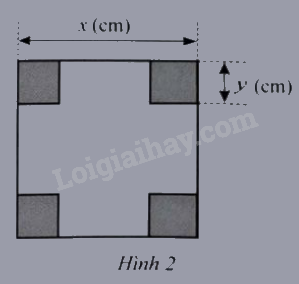
Một miếng bìa có dạng hình vuông với độ dài xạnh là (x) (cm).
Đề bài
Một miếng bìa có dạng hình vuông với độ dài xạnh là \(x\) (cm). Người ta cắt đi ở mỗi góc của miếng bìa một hình vuông sao cho bốn hình vuông bị cắt đi có cùng độ dài cạnh là \(y\) (cm) với \(0 < 2y < x\) (Hình 2).
a) Viết phân thức biểu thị tỉ số diện tích của miếng bìa ban đầu và phần miếng bìa còn lại sau khi bị cắt.
b) Tính giá trị của phân thức đó tại \(x = 4;y = 1\)
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích hình chữ nhật và công thức tính diện tích hình vuông để viết phân thức biểu thị tỉ số diện tích của miếng bìa ban đầu và phần miếng bìa còn lại sau khi bị cắt.
Lời giải chi tiết
a) Diện tích của miếng bìa ban đầu là: \({x^2}\left( {c{m^2}} \right)\)
Diện tích của phần bìa còn lại sau khi cắt là: \({x^2} - 4{y^2}\left( {c{m^2}} \right)\)
Phân thức biểu thị tỉ số diện tích của miếng bìa ban đầu và phần miếng bìa còn lại sau khi bị cắt là: \(\frac{{{x^2}}}{{{x^2} - 4{y^2}}}\)
b) Giá trị của phân thức \(\frac{{{x^2}}}{{{x^2} - 4{y^2}}}\) tại \(x = 4;y = 1\) là: \(\frac{{{4^2}}}{{{4^2} - {{4.1}^2}}} = \frac{4}{3}\)
Bài 8 trang 34 sách bài tập Toán 8 Cánh Diều thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về tính chất của hình thang cân, đặc biệt là tính chất về các cạnh đáy, các cạnh bên, các góc và đường chéo để giải quyết các bài toán thực tế.
Bài 8 trang 34 sách bài tập Toán 8 Cánh Diều thường bao gồm các dạng bài tập sau:
Đề bài: Cho hình thang cân ABCD (AB // CD). Gọi E là giao điểm của AD và BC. Chứng minh rằng EA = EB.
Lời giải:
Đề bài: Cho hình thang cân ABCD (AB // CD). Gọi M, N lần lượt là trung điểm của AD và BC. Chứng minh rằng MN là đường trung bình của hình thang.
Lời giải:
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 8 trang 34 sách bài tập Toán 8 Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!