Bài 26 trang 99 sách bài tập Toán 8 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 26 trang 99 sách bài tập Toán 8 - Cánh Diều, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài.
Cho hình thoi (ABCD) có góc (B) tù. Kẻ (BE) vuông góc (AD) tại (E), (BF) vuông góc với (CD) tại (F).
Đề bài
Cho hình thoi \(ABCD\) có góc \(B\) tù. Kẻ \(BE\) vuông góc \(AD\) tại \(E\), \(BF\) vuông góc với \(CD\) tại \(F\). Gọi \(M,N\) lần lượt là giao điểm của \(BE,BF\) với \(AC\). Chứng minh tứ giác \(BMDN\) là hình thoi.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất của hình thoi:
Trong một hình thoi:
- Các cạnh đối song song
- Các góc đối bằng nhau
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
- Hai đường chéo là các đường phân giác của các góc ở đỉnh.
Lời giải chi tiết
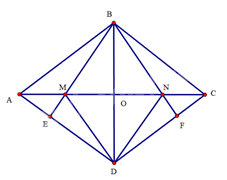
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
Do \(ABCD\) là hình thoi nên \(AC\) vuông góc với \(BD\) tại trung điểm \(O\) của \(BD\). Suy ra \(AC\) là đường trung trực của \(BD\). Do đó \(BM = DM,BN = DN\).
Do \(ABCD\) là hình thoi nên \(BA = BC,\widehat {BAE} = \widehat {BCF}\).
Suy ra \(\Delta ABE = \Delta BCF\) (cạnh huyền – góc nhọn kề)
Do đó \(\widehat {ABE} = \widehat {CBF}\). Mà \(\widehat {ABD} = \widehat {CBD}\), suy ra \(\widehat {MBO} = \widehat {NBO}\).
\(\Delta MBO = \Delta NBO\) (cạnh góc vuông – góc nhọn). suy ra \(BM = BN\)
Mà \(BM = DM\) và \(BN = DN\), suy ra \(BM = DM = BN = DN\).
Tứ giác \(BMDN\) có \(BM = DM = BN = DN\) nên \(BMDN\) là hình thoi.
Bài 26 trang 99 sách bài tập Toán 8 - Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng kiến thức về các tứ giác đặc biệt (hình bình hành, hình chữ nhật, hình thoi, hình vuông) để giải quyết các bài toán liên quan đến tính chất đường trung bình của tam giác, đường trung bình của hình thang và ứng dụng vào việc chứng minh các tính chất hình học.
Bài 26 thường bao gồm các dạng bài tập sau:
Để giải bài 26 trang 99 sách bài tập Toán 8 - Cánh Diều một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Dưới đây là hướng dẫn giải chi tiết một số dạng bài tập thường gặp trong bài 26:
Để chứng minh một tứ giác là hình bình hành, ta có thể sử dụng một trong các cách sau:
Để chứng minh một tứ giác là hình chữ nhật, ta có thể sử dụng một trong các cách sau:
Để chứng minh một tứ giác là hình thoi, ta có thể sử dụng một trong các cách sau:
Để chứng minh một tứ giác là hình vuông, ta có thể sử dụng một trong các cách sau:
Khi giải bài tập về các tứ giác đặc biệt, các em cần chú ý:
Việc giải bài 26 trang 99 sách bài tập Toán 8 - Cánh Diều giúp các em:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 26 trang 99 sách bài tập Toán 8 - Cánh Diều và đạt kết quả tốt trong môn Toán.