Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 66 trang 84 sách bài tập Toán 8 tập hai – Cánh diều. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với chương trình học Toán 8 hiện hành.
Cho điểm \(M\) thuộc đoạn thẳng \(AB\), với \(MA=a,MB=b\). Vẽ hai tam giác đều \(AMC\) và \(BMD\); gọi \(E\) là giao điểm của \(AD\) và \(CM\),
Đề bài
Cho điểm \(M\) thuộc đoạn thẳng \(AB\), với \(MA=a,MB=b\). Vẽ hai tam giác đều \(AMC\) và \(BMD\); gọi \(E\) là giao điểm của \(AD\) và \(CM\), \(F\) là giao điểm của \(DM\) và \(BC\) (Hình 58).
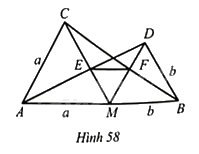
a) Chứng minh \(EF//AB\)
b) Tính \(ME,MF\) theo \(a,b\).
Phương pháp giải - Xem chi tiết
Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu:
\(\widehat{A'}=\widehat{A},\widehat{B'}=\widehat{B},\widehat{C'}=\widehat{C}\) ; \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}\).
Kí hiệu là \(\Delta A'B'C'\backsim \Delta ABC\).
Tỉ số các cạnh tương ứng \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=k\) gọi là tỉ số đồng dạng.
Lời giải chi tiết
a) Ta có \(\widehat{DMB}=\widehat{CAM}=60{}^\circ \), \(\widehat{DBM}=\widehat{CMA}=60{}^\circ \). Suy ra \(MD//AC,DB//CM\).
Do \(MD//AC\) nên \(\frac{EC}{EM}=\frac{AC}{DM}=\frac{a}{b}\) (theo định lí Thales)
Tương tự, do \(DB//CM\) nên \(\frac{CF}{FB}=\frac{CM}{DB}=\frac{a}{b}\)
Từ đó, ta có: \(\frac{EC}{EM}=\frac{CF}{FB}=\frac{a}{b}\) nên \(EF//MB\) hay \(EF//AB\)
b) Từ \(EF//AB\) suy ra tam giác \(EMF\) là tam giác đều.
Từ đó, ta có: \(\frac{EC=\frac{a}{a+b}}{CM}=\frac{EF}{MB}=\frac{EC+EF}{CM+MB}\)
\(=>EF=\frac{ab}{a+b}\)
Vì tam giác \(MEF\) là tam giác đều nên \(ME=MF=EF=\frac{ab}{a+b}\).
Bài 66 trang 84 sách bài tập Toán 8 – Cánh diều thuộc chương trình học về hình hộp chữ nhật và hình lập phương. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản sau:
Bài tập 66 trang 84 sách bài tập Toán 8 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giải bài tập 66 trang 84 sách bài tập Toán 8 – Cánh diều một cách hiệu quả, học sinh cần thực hiện theo các bước sau:
Bài tập: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 4cm và chiều cao 3cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật đó.
Giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 8 – Cánh diều và các tài liệu tham khảo khác.
Để học tốt môn Toán 8, học sinh cần:
Giaitoan.edu.vn là website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán từ lớp 6 đến lớp 12. Chúng tôi hy vọng sẽ là người bạn đồng hành đáng tin cậy trên con đường chinh phục môn Toán của bạn.