Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 31 trang 102 sách bài tập Toán 8 Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 31 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho hình vuông \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Trên tia đối của tia \(CB\) lấy điểm \(K\) sao cho \(BC = CK\).
Đề bài
Cho hình vuông \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Trên tia đối của tia \(CB\) lấy điểm \(K\) sao cho \(BC = CK\). Từ điểm \(B\) kẻ đường thẳng song song với \(AC\) cắt tia \(DC\) tại \(E\). Gọi \(F\) là trung điểm của \(BE\).
a) Chứng minh các tứ giác \(BOCF\) và \(BDKE\) đều là hình vuông.
b) Tứ giác \(CDOF\) có thể là hình vuông không? Vì sao?
Phương pháp giải - Xem chi tiết
Dựa vào dấu hiệu nhận biết của hình vuông:
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
- Hình chữ nhật có hai đường chéo là đường phân giác của một góc là hình vuông
Lời giải chi tiết
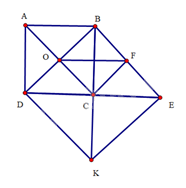
a) Tứ giác \(ABCD\) là hình vuông suy ra \(\widehat {ACB} = 45^\circ ,OB = OC,\widehat {BOC} = \widehat {DOC} = 90^\circ \).
Ta có: \(\widehat {BOF} = \widehat {DOC}\) (hai góc đồng vị) nên \(\widehat {OBF} = 90^\circ ;\widehat {CBE} = \widehat {ACB}\) (hai góc so le trong) nên \(\widehat {CBE} = 45^\circ \).
Từ đó ta chứng minh được tam giác \(BDE\) vuông cân tại \(B\) và tam giác \(BCE\) vuông cân tại \(C\). Suy ra \(BD = BE\) và \(BC = EC\).
\(\Delta BCF = \Delta ECF\) (c.c.c). Suy ra ta tính được \(\widehat {BFC} = \widehat {EFC} = 90^\circ \)
Tứ giác \(BOCF\) có \(\widehat {BOC} = \widehat {OBF} = \widehat {BFC} = 90^\circ \) nên \(BOCF\) là hình chữ nhật.
Hình chữ nhật \(BOCF\) có \(OB = OC\) nên \(BOCF\) là hình vuông.
Ta có: \(BC = CD\) và \(BC = CE\) nên \(CD = CE\).
Tứ giác \(BDKE\) có hai đường chéo \(BK\) và \(DE\) cắt nhau tại trung điểm \(C\) của mỗi đường nên \(BDKE\) là hình bình hành.
Hình bình hành \(BDKE\) có \(\widehat {DBE} = 90^\circ \)nên \(BDKE\) là hình chữ nhật
Hình chữ nhật \(BDKE\) có \(BD = BE\) nên \(BDKE\) là hình vuông
b) Tứ giác \(CDOF\) có \(\widehat {ODC} = 45^\circ \) nên \(CDOF\) không thể là hình vuông.
Bài 31 trang 102 sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững định nghĩa, tính chất của hình thang cân, cũng như các công thức tính diện tích, chu vi liên quan.
Bài 31 yêu cầu học sinh giải quyết các bài toán liên quan đến việc chứng minh một tứ giác là hình thang cân, tính độ dài các cạnh, đường cao, và diện tích của hình thang cân. Các bài toán thường được trình bày dưới dạng hình vẽ minh họa, đòi hỏi học sinh phải có khả năng quan sát, phân tích và áp dụng các kiến thức đã học để tìm ra lời giải.
Để giúp học sinh hiểu rõ hơn về cách giải bài 31, chúng ta sẽ đi qua từng phần của bài tập. Trước hết, cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu cần tìm. Sau đó, vẽ hình minh họa (nếu cần) và sử dụng các kiến thức về hình thang cân để tìm ra mối liên hệ giữa các yếu tố đã cho và yếu tố cần tìm.
Giả sử đề bài yêu cầu chứng minh tứ giác ABCD là hình thang cân, với AB song song CD và AD = BC. Để chứng minh điều này, ta có thể sử dụng định nghĩa của hình thang cân, đó là hình thang có hai cạnh bên bằng nhau. Ta có thể chứng minh AD = BC bằng cách sử dụng các tam giác đồng dạng hoặc các định lý về tam giác cân.
Kiến thức về hình thang cân có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, và thiết kế. Ví dụ, hình thang cân thường được sử dụng trong việc thiết kế mái nhà, cầu, và các công trình xây dựng khác.
Bài 31 trang 102 sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình thang cân. Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trên, các bạn học sinh sẽ tự tin hơn trong việc giải bài tập này và đạt kết quả tốt trong các bài kiểm tra. Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức thú vị khác trong môn Toán nhé!