Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1 trang 39 SGK Toán 12 tập 2 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập này thuộc chương trình học Toán 12 tập 2, tập trung vào các kiến thức về tích phân.
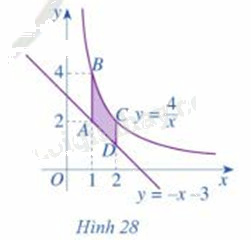
Hình thang cong ABCD ở Hình 28 có diện tích bằng: A. (intlimits_1^2 {left( {frac{4}{x} - x + 3} right)dx} ) B. (intlimits_1^2 {left( {frac{4}{x} + x + 3} right)dx} ) C. (intlimits_1^2 {left( {frac{4}{x} - x - 3} right)dx} ) D. (intlimits_2^4 {left( {frac{4}{x} + x + 3} right)dx} )
Đề bài
Hình thang cong ABCD ở Hình 28 có diện tích bằng:
A. \(\int\limits_1^2 {\left( {\frac{4}{x} - x + 3} \right)dx} \)
B. \(\int\limits_1^2 {\left( {\frac{4}{x} + x + 3} \right)dx} \)
C. \(\int\limits_1^2 {\left( {\frac{4}{x} - x - 3} \right)dx} \)
D. \(\int\limits_2^4 {\left( {\frac{4}{x} + x + 3} \right)dx} \)
Phương pháp giải - Xem chi tiết
Cho hàm số y = f(x), y = g(x) liên tục trên đoạn [a;b]. Khi đó, diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b là: \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \)
Lời giải chi tiết
Diện tích hình thang cong đó là: \(\int\limits_1^2 {\left| {\frac{4}{x} - \left( { - x - 3} \right)} \right|dx} = \int\limits_1^2 {\left| {\frac{4}{x} + x + 3} \right|dx} = \int\limits_1^2 {\left( {\frac{4}{x} + x + 3} \right)dx} \)
Chọn B
Bài tập 1 trang 39 SGK Toán 12 tập 2 - Cánh diều yêu cầu học sinh vận dụng kiến thức về tích phân để tính diện tích hình phẳng. Đây là một dạng bài tập quan trọng, thường xuyên xuất hiện trong các kỳ thi THPT Quốc gia. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về tích phân, phương pháp tính tích phân và các công thức liên quan.
Bài tập 1 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính diện tích các hình phẳng giới hạn bởi các đường cong và trục tọa độ. Cụ thể, bài tập yêu cầu tính diện tích hình phẳng giới hạn bởi:
Để giải bài tập 1 trang 39 SGK Toán 12 tập 2 - Cánh diều, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đường cong y = x2, trục Ox và hai đường thẳng x = 0, x = 2.
Giải:
Diện tích hình phẳng S được tính bằng công thức:
S = ∫02 x2 dx
S = [x3/3]02 = (23/3) - (03/3) = 8/3
Vậy diện tích hình phẳng là 8/3.
Để củng cố kiến thức và kỹ năng giải bài tập về tích phân, học sinh có thể tự giải các bài tập sau:
Bài tập 1 trang 39 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng, giúp học sinh rèn luyện kỹ năng tính tích phân và ứng dụng vào việc giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi đối mặt với bài tập này và các bài tập tương tự trong các kỳ thi sắp tới.