Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các câu hỏi trong sách giáo khoa Toán 12 tập 1, trang 89, thuộc bộ sách Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập. Hãy cùng khám phá lời giải chi tiết ngay sau đây!
Xét mẫu số liệu ghép nhóm cho bởi bảng 13 a) Tìm \({x_1},{x_2},{x_3},{x_4},{x_5}\) lần lượt là giá trị đại diện của nhóm 1, nhóm 2, nhóm 3, nhóm 4, nhóm 5 b) Tính số trung bình cộng \(\overline x \) của mẫu số liệu ghép nhóm đó c) Tính \({s^2} = \frac{{3.{{({x_1} - \overline x )}^2} + 12{{({x_2} - \overline x )}^2} + 9{{({x_3} - \overline x )}^2} + 7{{({x_4} - \overline x )}^2} + 9{{({x_5} - \overline x )}^2}}}{{40}}\) d) Tính \(s = \sqrt {{s^2}} \)
Đề bài
Xét mẫu số liệu ghép nhóm cho bởi bảng 13
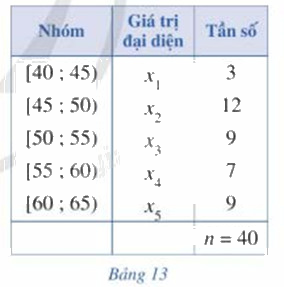
a) Tìm \({x_1},{x_2},{x_3},{x_4},{x_5}\) lần lượt là giá trị đại diện của nhóm 1, nhóm 2, nhóm 3, nhóm 4, nhóm 5
b) Tính số trung bình cộng \(\overline x \) của mẫu số liệu ghép nhóm đó
c) Tính \({s^2} = \frac{{3.{{({x_1} - \overline x )}^2} + 12{{({x_2} - \overline x )}^2} + 9{{({x_3} - \overline x )}^2} + 7{{({x_4} - \overline x )}^2} + 9{{({x_5} - \overline x )}^2}}}{{40}}\)
d) Tính \(s = \sqrt {{s^2}} \)
Phương pháp giải - Xem chi tiết
Quan sát bảng số liệu và áp dụng công thức
Lời giải chi tiết
a) \({x_1} = 42,5;{x_2} = 47,5;{x_3} = 52,5;{x_4} = 57,5;{x_5} = 62,5\)
b) \(\overline x = \frac{{3.42,5 + 12.47,5 + 9.52,5 + 7.57,5 + 9.62,5}}{{40}} = 53,375\)
c) \({s^2} = \frac{{3.{{({x_1} - \overline x )}^2} + 12{{({x_2} - \overline x )}^2} + 9{{({x_3} - \overline x )}^2} + 7{{({x_4} - \overline x )}^2} + 9{{({x_5} - \overline x )}^2}}}{{40}}\)
\( = \frac{{3.{{(42,5 - 53,375)}^2} + 12{{(47,5 - 53,375)}^2} + 9{{(52,5 - 53,375)}^2} + 7{{(57,5 - 53,375)}^2} + 9{{(62,5 - 53,375)}^2}}}{{40}}\)
\( = \frac{{2631}}{{64}}\)
d) \(s = \sqrt {{s^2}} = \sqrt {\frac{{2631}}{{64}}} \approx 6,41\)
Trang 89 SGK Toán 12 tập 1 - Cánh diều tập trung vào các bài tập liên quan đến đạo hàm của hàm số. Cụ thể, các bài tập này yêu cầu học sinh vận dụng các quy tắc tính đạo hàm cơ bản, đạo hàm của hàm hợp, và đạo hàm của hàm lượng giác để giải quyết các bài toán thực tế. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để học tốt các chương trình Toán học nâng cao hơn.
Chúng ta sẽ đi vào giải chi tiết từng bài tập trong trang 89 SGK Toán 12 tập 1 - Cánh diều:
Lời giải:
Lời giải:
Sử dụng quy tắc đạo hàm hàm hợp: y' = 2(x2 + 1) * 2x = 4x(x2 + 1)
Lời giải:
Sử dụng quy tắc đạo hàm hàm hợp: f'(x) = cos(2x) * 2 = 2cos(2x)
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Để hiểu sâu hơn về đạo hàm và các ứng dụng của nó, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em học sinh đã có thể tự tin giải quyết các bài tập trang 89 SGK Toán 12 tập 1 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao!