Đường tiệm cận là một khái niệm quan trọng trong chương trình Toán 12, đặc biệt là khi nghiên cứu về đồ thị hàm số. Nắm vững lý thuyết này giúp học sinh hiểu rõ hơn về hành vi của hàm số khi x tiến tới vô cùng hoặc một giá trị cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ và chi tiết về lý thuyết đường tiệm cận, phù hợp với chương trình Toán 12 Cánh Diều. Hãy cùng khám phá ngay!
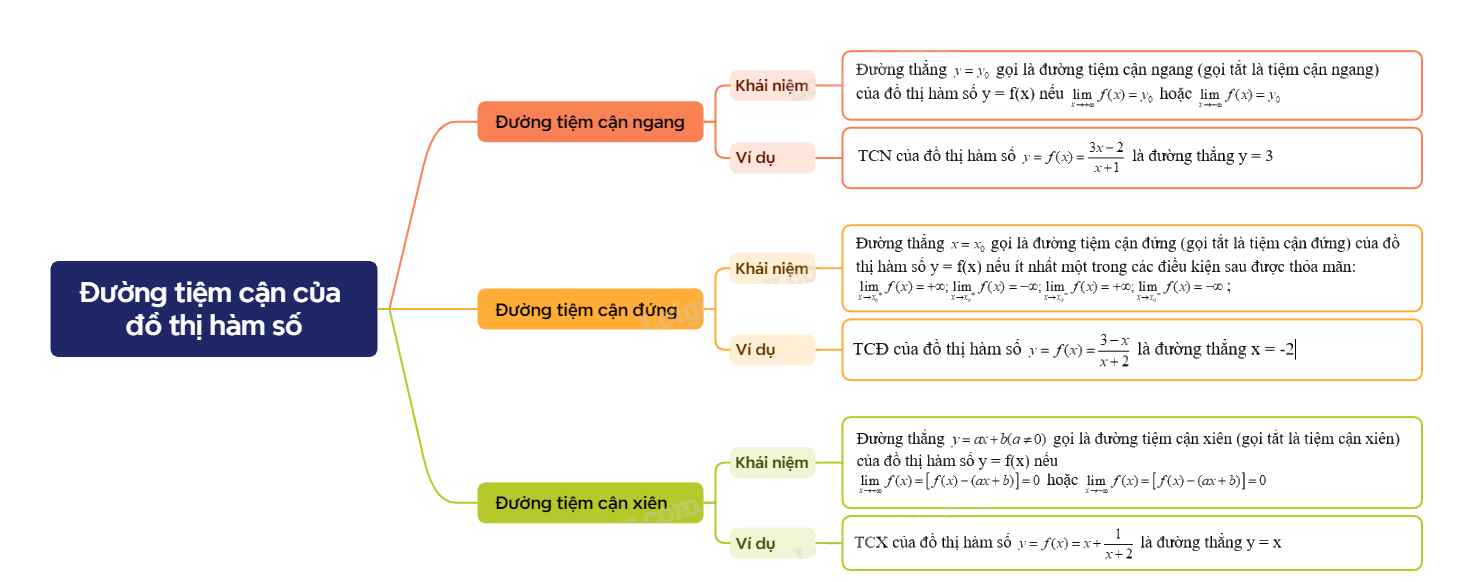
1. Đường tiệm cận ngang
1. Đường tiệm cận ngang
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\) |
Ví dụ: Tìm TCN của đồ thị hàm số \(y = f(x) = \frac{{3x - 2}}{{x + 1}}\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{x + 1}} = 3\)
Vậy đồ thị hàm số f(x) có TCN là y = 3.
2. Đường tiệm cận đứng
Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \); |
Ví dụ: Tìm TCĐ của đồ thị hàm số \(y = f(x) = \frac{{3 - x}}{{x + 2}}\)
Ta có: \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{3x - 2}}{{x + 2}} = + \infty \)
Vậy đồ thị hàm số có TCĐ là x = -2
3.Đường tiệm cận xiên
Đường thẳng \(y = ax + b(a \ne 0)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\) |
Ví dụ: Tìm TCX của đồ thị hàm số \(y = f(x) = x + \frac{1}{{x + 2}}\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 2}} = 0\)
Vậy đồ thị hàm số có TCX là y = x
Đường tiệm cận là đường thẳng mà đồ thị của hàm số tiến gần đến khi x hoặc y tiến tới vô cùng. Việc hiểu rõ các loại đường tiệm cận và cách xác định chúng là nền tảng quan trọng để phân tích và vẽ đồ thị hàm số.
Đường tiệm cận của đồ thị hàm số y = f(x) là đường thẳng mà khoảng cách từ một điểm bất kỳ trên đồ thị hàm số đến đường thẳng đó tiến tới 0 khi x hoặc y tiến tới vô cùng.
Để xác định đường tiệm cận, ta cần thực hiện các bước sau:
Xét hàm số y = (2x + 1) / (x - 1).
Hãy xác định đường tiệm cận của các hàm số sau:
Không phải hàm số nào cũng có đường tiệm cận. Một hàm số có thể có một, hai hoặc ba loại đường tiệm cận khác nhau. Việc hiểu rõ các khái niệm và phương pháp xác định đường tiệm cận là rất quan trọng để giải các bài toán liên quan đến đồ thị hàm số.
Đường tiệm cận giúp chúng ta:
Hy vọng với những kiến thức trên, bạn đã nắm vững lý thuyết về đường tiệm cận của đồ thị hàm số Toán 12 Cánh Diều. Chúc bạn học tập tốt!