Công thức xác suất toàn phần và công thức Bayes là những công cụ quan trọng trong việc giải quyết các bài toán xác suất phức tạp, đặc biệt trong chương trình Toán 12 Cánh Diều. Nắm vững hai công thức này giúp học sinh có thể tính toán xác suất của một sự kiện khi thông tin về sự kiện đó được cung cấp gián tiếp thông qua các sự kiện khác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lý thuyết đầy đủ, ví dụ minh họa chi tiết và bài tập thực hành đa dạng để bạn có thể hiểu sâu sắc và áp dụng thành thạo hai công thức này.
1. Công thức xác suất toàn phần
1. Công thức xác suất toàn phần
Cho hai biến cố A và B với 0 < P(B) < 1. Khi đó \(P(A) = P(A \cap B) + (A \cap \overline B ) = P(B).P(A|B) + P(\overline B ).P(A|\overline B )\) gọi là công thức xác suất toàn phần. |
Ví dụ 1: Theo một số liệu thống kê, năm 2004 ở Canada có 65% nam giới là thừa cân và 53,4% nữ giới là thừa cân. Nam giới và nữ giới ở Canada đều chiếm 50% dân số cả nước (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Springer, 2005). Hỏi rằng, trong năm 2004, xác suất để một người Canada được chọn ngẫu nhiên là người thừa cân bằng bao nhiêu?
Giải:
Xét hai biến cố sau:
A: “Người được chọn ra là người thừa cân”;
B: “Người được chọn ra là nam giới” (biến cố \(\overline B \): “Người được chọn ra là nữ giới”).
Từ giả thiết ta có:
\(P(B) = P(\overline B ) = 50\% = 0,5\); \(P(A|B) = 65\% = 0,65\), \(P(A|\overline B ) = 53,4\% = 0,534\).
Theo công thức xác suất toàn phần, ta có:
\(P(A) = P(B).P(A|B) + P(\overline B ).P(A|\overline B ) = 0,5.0,65 + 0,5.0,534 = 0,592\).
Vậy xác suất để một người Canada được chọn ngẫu nhiên là người thừa cân bằng 0,592.
Lối cách khác, tỉ lệ người Canada thừa cân là 59,2%.
Ví dụ 2: Trong trò chơi hái hoa có thưởng của lớp 12A, cô giáo treo 10 bông hoa trên cành cây, trong đó có 5 bông hoa chưa phiếu có thưởng. Bạn Bình hái bông hoa đầu tiên sau đó bạn An hái bông hoa thứ hai.
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Từ đó, tính xác suất bạn An hái được bông hoa chứa phiếu có thưởng.
Giải:
Xét hai biến cố:
A: “Bông hoa bạn An hái được chứa phiếu có thưởng”.
B: “Bông hoa bạn Bình hái được chứa phiếu có thưởng”.
Khi đó, ta có:
\(P(B) = \frac{5}{{10}} = \frac{1}{2}\), \(P(\overline B ) = 1 - P(B) = 1 - \frac{1}{2} = \frac{1}{2}\), \(P(A|B) = \frac{4}{9}\), \(P(A|\overline B ) = \frac{5}{9}\).
a) Sơ đồ hình cây biểu thị tình huống đã cho là:
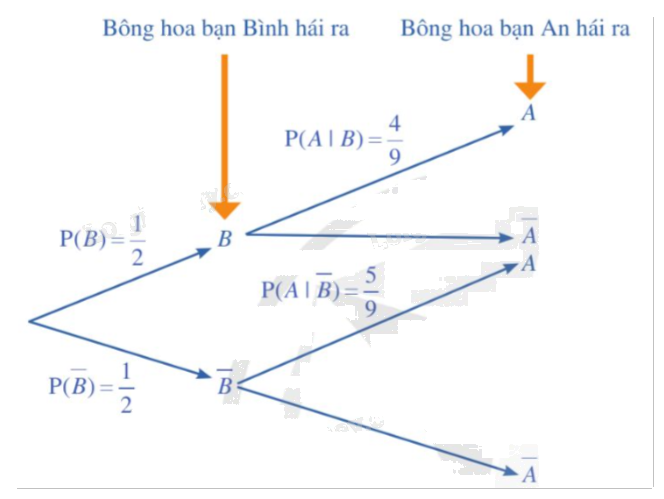
b) Áp dụng công thức xác suất toàn phần, ta có:
\(P(A) = P(B).P(A|B) + P(\overline B ).P(A|\overline B ) = \frac{1}{2}.\frac{4}{9} + \frac{1}{2}.\frac{5}{9} = \frac{1}{2}\).
Vậy xác suất bạn An hái được bông hoa chứa phiếu có thưởng bằng \(\frac{1}{2}\).
2. Công thức Bayes
Với hai biến cố A, B mà P(A) > 0 và P(B) > 0. Khi đó \(P(B|A) = \frac{{P(B).P(A|B)}}{{P(A)}}\) gọi là công thức Bayes. |
Nhận xét: Cho hai biến cố A, B với P(A) > 0, 0 < P(B) < 1. Do \(P(A) = P(A \cap B) + (A \cap \overline B ) = P(B).P(A|B) + P(\overline B ).P(A|\overline B )\)nên công thức Bayes còn có dạng \(P(B|A) = \frac{{P(B).P(A|B)}}{{P(B).P(A|B) + P(\overline B ).P(A|\overline B )}}\).
Ví dụ 1: Cho hai biến cố A, B sao cho P(A) = 0,6; P(B) = 0,4; P(A|B) = 0,3. Tính P(B|A).
Giải:
Áp dụng công thức Bayes, ta có: \(P(B|A) = \frac{{P(B).P(A|B)}}{{P(A)}} = \frac{{0,4.0,3}}{{0,6}} = 0,2\).
Ví dụ 2: Giả sử có một loại bệnh mà tỷ lệ người mắc bệnh là 0,1%. Giả sử có một loại xét nghiệm, mà ai mắc bệnh khi xét nghiệm cũng có phản ứng dương tính, nhưng tỷ lệ phản ứng dương tính giả là 5% (tức là trong số những người không bị bệnh có 5% số người xét nghiệm lại có phản ứng dương tính).
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Khi một người xét nghiệm có phản ứng dương tính thì khả năng mắc bệnh của người đó bao nhiêu phần trăm (làm tron kết quả đánh hàng phần trăm)?
Giải:
a) Xét hai biến cố:
K: “Người được chọn ra không mắc bệnh”.
D: “Người được chọn ra có phản ứng dương tính”.
Do tỷ lệ mắc bệnh là 0,1% = 0,001 nên P(K) = 1 - 0,001 = 0,999.
Trong số những người mắc bệnh có 5% số người có phản ứng dương tính nên P(D|K) = 5% = 0,05. Vì ai mắc bệnh khi xét nghiệm cũng phản ứng dương tính nên \(P(D|\overline K ) = 1\).
Sơ đồ hình cây ở Hình 3 biểu thị tình huống đã cho.
b) Ta thấy: Khả năng mắc bệnh của một người xét nghiệm có phản ứng dương tính chính là \(P(\overline K |D)\). Áp dụng công thức Bayes, ta có:
\(P(\overline K |D) = \frac{{P(\overline K ).P(D|\overline K )}}{{P(\overline K ).P(D|\overline K ) + P(K).P(D|K)}} = \frac{{0,001}}{{0,001 + 0,999.0,05}} = 1,96\% \).
Vậy xác suất mắc bệnh của một người xét nghiệm có phản ứng dương tính là 1,96%.

Trong chương trình Toán 12, đặc biệt là với sách Cánh Diều, việc nắm vững lý thuyết xác suất là vô cùng quan trọng. Hai công thức then chốt trong phần này là công thức xác suất toàn phần và công thức Bayes. Chúng không chỉ xuất hiện trong các bài kiểm tra, thi cử mà còn có ứng dụng thực tế cao trong nhiều lĩnh vực.
Công thức xác suất toàn phần được sử dụng để tính xác suất của một sự kiện A khi sự kiện đó có thể xảy ra thông qua một số các sự kiện khác, không loại trừ lẫn nhau.
Phát biểu: Nếu B1, B2, ..., Bn là một hệ các sự kiện không loại trừ lẫn nhau và B1 ∪ B2 ∪ ... ∪ Bn = Ω (không gian mẫu), thì xác suất của sự kiện A được tính theo công thức:
P(A) = P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bn)P(Bn)
Ví dụ: Một nhà máy có hai dây chuyền sản xuất. Dây chuyền 1 sản xuất 60% tổng số sản phẩm và tỷ lệ sản phẩm lỗi là 2%. Dây chuyền 2 sản xuất 40% tổng số sản phẩm và tỷ lệ sản phẩm lỗi là 3%. Tính xác suất một sản phẩm được chọn ngẫu nhiên là sản phẩm lỗi.
Giải:
P(A) = P(A|B1)P(B1) + P(A|B2)P(B2) = 0.02 * 0.6 + 0.03 * 0.4 = 0.012 + 0.012 = 0.024
Công thức Bayes được sử dụng để tính xác suất có điều kiện của một sự kiện khi biết thông tin về một sự kiện khác liên quan đến nó.
Phát biểu: Nếu B1, B2, ..., Bn là một hệ các sự kiện không loại trừ lẫn nhau và B1 ∪ B2 ∪ ... ∪ Bn = Ω, thì xác suất có điều kiện của Bi khi biết A xảy ra được tính theo công thức:
P(Bi|A) = [P(A|Bi)P(Bi)] / P(A)
Trong đó P(A) được tính theo công thức xác suất toàn phần.
Ví dụ: Sử dụng dữ liệu từ ví dụ trên, tính xác suất một sản phẩm lỗi được sản xuất từ dây chuyền 1.
Giải:
P(B1|A) = [P(A|B1)P(B1)] / P(A) = (0.02 * 0.6) / 0.024 = 0.012 / 0.024 = 0.5
Hai công thức này có nhiều ứng dụng trong thực tế, bao gồm:
Để hiểu rõ hơn về hai công thức này, bạn nên thực hành giải nhiều bài tập khác nhau. Dưới đây là một số bài tập gợi ý:
Hy vọng với những kiến thức và ví dụ trên, bạn đã có cái nhìn tổng quan về lý thuyết công thức xác suất toàn phần và công thức Bayes trong chương trình Toán 12 Cánh Diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng thành thạo vào giải quyết các bài toán thực tế.