Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài tập 9 trang 41 SGK Toán 12 tập 2 theo chương trình Cánh diều.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn nắm vững kiến thức Toán học.
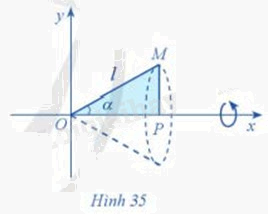
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Giả sử \(\widehat {POM} = \alpha ,OM = l(0 \le \alpha \le \frac{\pi }{3};l > 0)\). Gọi \({\rm N}\) là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (Hình 35). Tính thể tích của \({\rm N}\) theo \(\alpha \) và \(l\)
Đề bài
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Giả sử \(\widehat {POM} = \alpha ,OM = l(0 \le \alpha \le \frac{\pi }{3};l > 0)\). Gọi \({\rm N}\) là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (Hình 35). Tính thể tích của \({\rm N}\) theo \(\alpha \) và \(l\)
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích hình nón
Lời giải chi tiết
Xét tam giác vuông OPM:
\(MP = OM.\sin \widehat {POM} = l.\sin \alpha \)
\(OP = OM.\cos \widehat {POM} = l.\cos \alpha \)
Khối tròn xoay là một hình nón có diện tích là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {\left( {l.\sin \alpha } \right)^2}.l.\cos \alpha = \frac{1}{3}\pi {l^3}.{\sin ^2}\alpha \cos \alpha \)
Bài tập 9 trang 41 SGK Toán 12 tập 2 thuộc chương trình Cánh diều, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của đại lượng. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài tập 9 thường có dạng như sau: Một vật thể chuyển động theo một quỹ đạo được mô tả bởi hàm số vị trí s(t). Yêu cầu là tìm vận tốc và gia tốc của vật thể tại một thời điểm cụ thể, hoặc xác định thời điểm vật thể đạt vận tốc cực đại/cực tiểu.
Đề bài: Một vật thể chuyển động theo hàm số vị trí s(t) = t3 - 6t2 + 9t + 2 (trong đó s tính bằng mét và t tính bằng giây). Tìm vận tốc và gia tốc của vật thể tại thời điểm t = 2 giây.
Giải:
Kết luận: Tại thời điểm t = 2 giây, vận tốc của vật thể là -3 m/s và gia tốc là 0 m/s2.
Ngoài dạng bài tập tìm vận tốc và gia tốc tại một thời điểm cụ thể, bài tập 9 trang 41 SGK Toán 12 tập 2 - Cánh diều còn có thể xuất hiện các dạng bài tập khác như:
Để giải quyết các dạng bài tập này, bạn cần vận dụng các kiến thức về đạo hàm, cực trị, và khoảng đơn điệu của hàm số một cách linh hoạt.
Ngoài SGK Toán 12 tập 2 - Cánh diều, bạn có thể tham khảo thêm các tài liệu sau để hỗ trợ học tập:
Bài tập 9 trang 41 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn khi giải quyết các bài tập tương tự.