Chào mừng bạn đến với bài học về lý thuyết phương trình mặt phẳng trong chương trình Toán 12 Cánh Diều. Đây là một phần kiến thức quan trọng trong hình học không gian, giúp bạn hiểu rõ hơn về vị trí tương quan giữa các mặt phẳng và đường thẳng trong không gian.
Bài học này sẽ cung cấp đầy đủ các khái niệm, định lý và công thức cần thiết để bạn có thể giải quyết các bài toán liên quan đến phương trình mặt phẳng một cách hiệu quả.
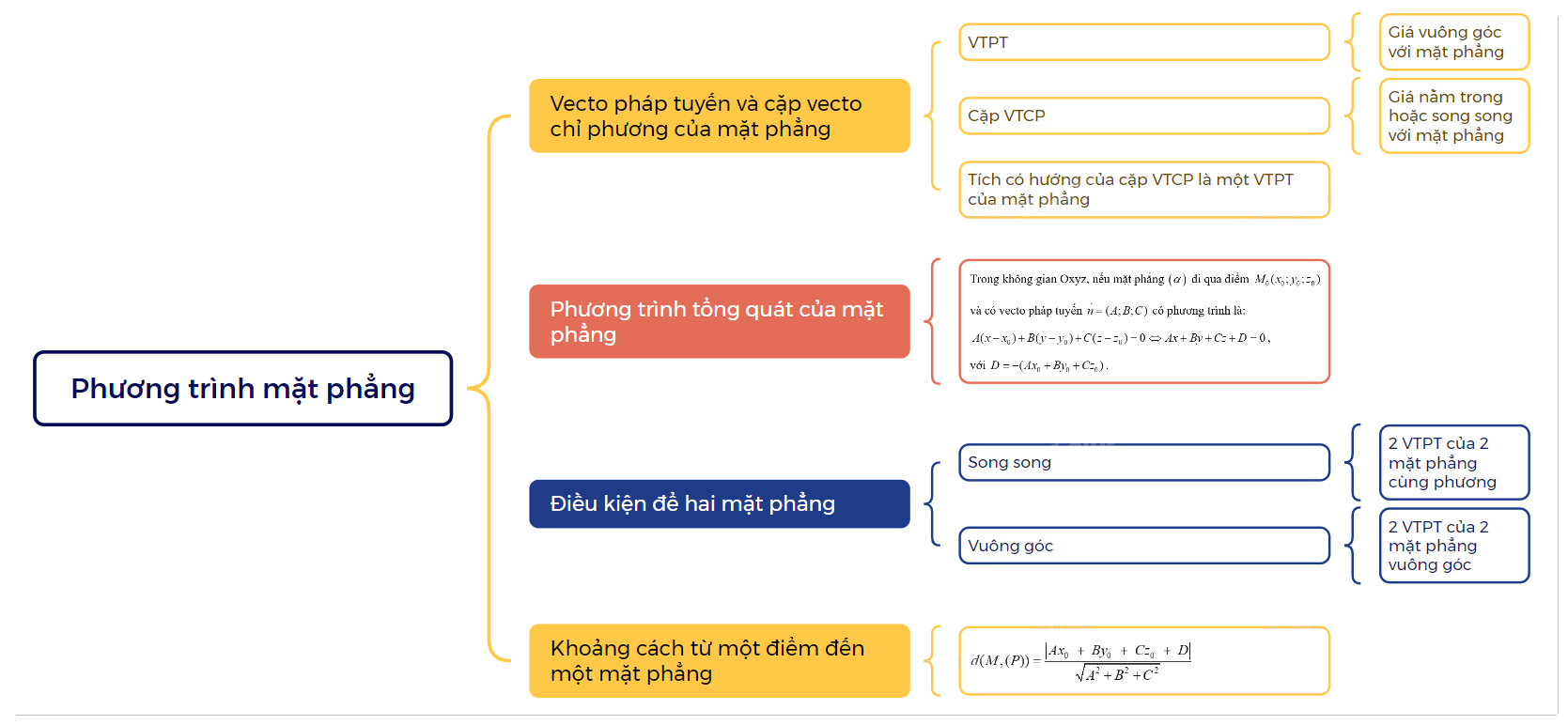
1. Vecto pháp tuyến, cặp vecto chỉ phương của mặt phẳng a) Vecto pháp tuyến
1. Vecto pháp tuyến, cặp vecto chỉ phương của mặt phẳng
a) Vecto pháp tuyến
| Vecto \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vecto pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\). |
b) Cặp vecto chỉ phương
| Cho mặt phẳng (P). Hai vecto không cùng phương có giá song song hoặc nằm trong mặt phẳng (P) được gọi là cặp vecto chỉ phương của mặt phẳng (P). |
c) Xác định vecto pháp tuyến của mặt phẳng khi biết cặp vecto chỉ phương
| Nếu hai vecto \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\) là cặp vecto chỉ phương của mặt phẳng (P) thì \(\overrightarrow n = \left[ {\overrightarrow a ;\overrightarrow b } \right] = \left( {\left| {\begin{array}{*{20}{c}}{{a_2}}&{{a_3}}\\{{b_2}}&{{b_3}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{a_3}}&{{a_1}}\\{{b_3}}&{{b_1}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|} \right)\). |
2. Phương trình tổng quát của mặt phẳng
| Trong không gian Oxyz, mỗi mặt phẳng đều có phương trình dạng Ax + By + Cz + D = 0, trong đó A, B, C không đồng thời bằng 0, được gọi là phương trình tổng quát của mặt phẳng đó. |
3. Lập phương trình tổng quát của mặt phẳng
Trong không gian Oxyz, nếu mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vecto pháp tuyến \(\overrightarrow n = (A;B;C)\) có phương trình là: \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0 \Leftrightarrow Ax + By + Cz + D = 0\), với \(D = - (A{x_0} + B{y_0} + C{z_0})\). |
Bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vecto chỉ phương:
Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vecto chỉ phương \(\overrightarrow u \), \(\overrightarrow v \) có thể thực hiện theo các bước sau:
- Tìm vecto pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
- Lập phương trình tổng quát của mặt phẳng đi qua M và biết vecto pháp tuyến \(\overrightarrow n \).
Bài toán viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng:
Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:
- Tìm cặp vecto chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \).
- Tìm vecto pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
- Lập phương trình tổng quát của mặt phẳng đi qua A và biết vecto pháp tuyến \(\overrightarrow n \).
4. Điều kiện để hai mặt phẳng vuông góc với nhau
Trong không gian Oxyz, cho hai mặt phẳng: \(\left( \alpha \right):Ax + By + Cz + D = 0,\left( \beta \right):A'x + B'y + C'z + D' = 0,\) với hai vecto pháp tuyến \(\overrightarrow n = (A;B;C)\), \(\overrightarrow {n'} = (A';B';C')\) tương ứng. Khi đó: \(\left( \alpha \right) \bot \left( \beta \right) \Leftrightarrow \overrightarrow n \bot \overrightarrow {n'} \Leftrightarrow AA' + BB' + CC' = 0\). |
5. Điều kiện để hai mặt phẳng song song với nhau
Trong không gian Oxyz, cho hai mặt phẳng: \(\left( \alpha \right):Ax + By + Cz + D = 0,\left( \beta \right):A'x + B'y + C'z + D' = 0,\) với hai vecto pháp tuyến \(\overrightarrow n = (A;B;C)\), \(\overrightarrow {n'} = (A';B';C')\) tương ứng. Khi đó: \(\left( \alpha \right)//\left( \beta \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {n'} = k\overrightarrow n \\D' \ne kD\end{array} \right.\) với k nào đó. |
6. Khoảng cách từ một điểm đến một mặt phẳng
Trong không gian Oxyz, khoảng cách từ điểm \({M_0}({x_0};{y_0};{z_0})\) đến mặt phẳng (P): Ax + By + Cz + D = 0 là: \(d(M,(P)) = \frac{{\left| {A{x_0}{\rm{ }} + {\rm{ }}B{y_0}{\rm{ }} + {\rm{ }}C{z_0}{\rm{ }} + {\rm{ }}D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\) |
Phương trình mặt phẳng là một công cụ quan trọng trong hình học không gian, cho phép chúng ta mô tả vị trí của một mặt phẳng trong không gian Oxyz. Hiểu rõ lý thuyết này là nền tảng để giải quyết các bài toán phức tạp hơn về hình học không gian.
Một mặt phẳng trong không gian được xác định duy nhất bởi một điểm thuộc mặt phẳng và một vectơ pháp tuyến của mặt phẳng. Vectơ pháp tuyến là vectơ vuông góc với mọi vectơ nằm trong mặt phẳng.
Cho mặt phẳng (P) đi qua điểm M0(x0, y0, z0) và có vectơ pháp tuyến n = (a, b, c). Phương trình tổng quát của mặt phẳng (P) là:
a(x - x0) + b(y - y0) + c(z - z0) = 0
Phương trình này có thể được viết lại dưới dạng:
ax + by + cz + d = 0, với d = -ax0 - by0 - cz0
Nếu vectơ pháp tuyến n = (a, b, c) có độ dài bằng 1 (tức là a2 + b2 + c2 = 1), thì phương trình ax + by + cz + d = 0 được gọi là phương trình chính tắc của mặt phẳng.
Để tìm phương trình mặt phẳng, ta cần xác định một điểm thuộc mặt phẳng và một vectơ pháp tuyến của mặt phẳng. Dưới đây là một số trường hợp thường gặp:
Xét mặt phẳng (P): ax + by + cz + d = 0 và đường thẳng (d): x = x0 + at, y = y0 + bt, z = z0 + ct.
Đường thẳng (d) và mặt phẳng (P) có các vị trí tương quan sau:
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về lý thuyết phương trình mặt phẳng trong chương trình Toán 12 Cánh Diều. Chúc bạn học tập tốt!