Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2, trang 58, 59 và 60 của sách giáo khoa Toán 12 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Các phép toán vecto trong không gian
Trả lời câu hỏi Hoạt động 5 trang 60 SGK Toán 12 Cánh diều
Nêu định nghĩa tích của một số thực \(k \ne 0\;\)với vecto\(\;\vec a\; \ne \vec 0\) trong mặt phẳng.
Lời giải chi tiết:
Cho số thực \(k \ne 0\) và \(vecto\;\vec a \ne \vec 0\). Tích của số k với vecto \(\vec a\) là một vecto, kí hiệu là \(k\vec a,\;\)được xác định như sau:
- Cùng hướng với vecto \(\vec a\) nếu k > 0, ngược hướng với vecto \(\vec a\) nếu k < 0.
- Có độ dài bằng \(\left| k \right|.\left| {\vec a} \right|\).
Trả lời câu hỏi Hoạt động 3 trang 59 SGK Toán 12 Cánh diều
Cho hình hộp ABCD.A’B’C’D’. Tìm liên hệ giữa \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} ;\;\overrightarrow {AC} + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \).
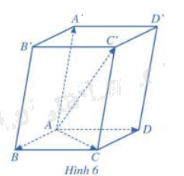
Phương pháp giải:
Áp dụng quy tắc ba điểm.
Lời giải chi tiết:
Áp dụng quy tắc ba điểm ta thấy:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {BD} \) (1)
Mà từ hình vẽ ta thấy \(\overrightarrow {BD} = \overrightarrow {AC} \;\;\;\;\;\;\;\;\left( 2 \right)\)
Từ (1) (2) => \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {A'C} \) (3)
Mà \(\overrightarrow {A'C} = \overrightarrow {AC'} \) (4)
Từ (3), (4) suy ra \(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Trả lời câu hỏi Hoạt động 7 trang 61 SGK Toán 12 Cánh diều
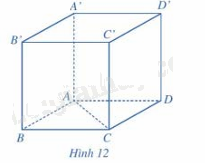
Trong không gian, cho hình lập phương ABCD.A’B’C’D’ có độ dài bằng 3cm (hình 12).
a) Tính góc giữa hai vecto \(\overrightarrow {AC} ,\overrightarrow {A'D'} \).
b) Tính \(\left| {\overrightarrow {AC} } \right|,\left| {\overrightarrow {A'D'} } \right|\). Cos(\(\overrightarrow {AC} ,\overrightarrow {A'D'} \)).
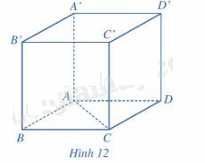
Phương pháp giải:
Áp dụng quy tắc 3 điểm và vectơ trong không gian.
Lời giải chi tiết:
Ta có A’D’//AD.
Góc giữa \(\overrightarrow {AC} \;\)và\(\;\overrightarrow {A'D'} \)= \(\;\overrightarrow {AC} \) và \(\overrightarrow {AD} \).
a) Mà ABCD là hình vuông => \(\widehat {CAD} = 45^\circ \)
b) \(\overrightarrow {\left| {AC} \right|} .|\overrightarrow {A'D'|} \) = AC.AD = 3.3 = 9.
cos(\(\overrightarrow {AC} ,\overrightarrow {A'D'} \))= cos(\(\overrightarrow {AC} ,\overrightarrow {AD} )\)= \(\frac{{\overrightarrow {AC} .\overrightarrow {AD} }}{{\overrightarrow {\left| {AC} \right|} .\overrightarrow {\left| {AD} \right|} }} = \frac{{3.3}}{{3.3}} = 1\).
Trả lời câu hỏi Hoạt động 4 trang 59 SGK Toán 12 Cánh diều
Trong không gian , cho hai vecto\(\;\vec a,\vec b.\;\) Lấy một điểm M tùy ý.
a) Vẽ \(\overrightarrow {MA} = \vec a,\;\overrightarrow {MB} = \vec b\;,\overrightarrow {MC} = \overrightarrow { - b} \).
b) Tổng của hai vecto \(\vec a\;\)và \(\;\overrightarrow { - b} \) bằng vecto nào trong hình 7.
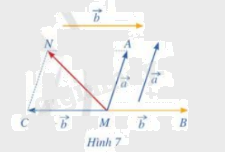
Phương pháp giải:
Sử dụng quy tắc hình bình hành.
Lời giải chi tiết:
\( \vec{a}\) + (\( - \vec{b}) =\) \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MN} \) (quy tắc hình bình hành).
Trả lời câu hỏi Hoạt động 2 trang 58 SGK Toán 12 Cánh diều
Trong không gian, cho 2 vec tơ \(\vec a\) và \(\vec b\). Lấy một điểm A tùy ý.
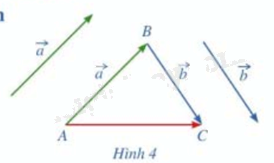
a) Vẽ \(\overrightarrow {AB} \)\( = \vec a\),\(\overrightarrow {BC} \)\( = \vec b\)
b) Tổng của 2 vec tơ \(\vec a\)và\(\vec b\) bằng vec tơ nào trong hình 4?
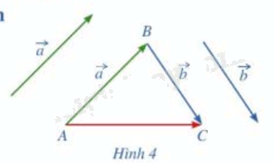
Phương pháp giải:
a) Ghi rõ các bước để vẽ hình
b) Áp dụng quy tắc 3 điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
a)
– Qua A vẽ một đường thẳng song song với \(\vec a\). Trên đường thẳng đó lấy điểm B sao cho \(AB = \left| {\vec a} \right|\) và \(\overrightarrow {AB}\) cùng hướng với \({\vec a}\).
– Qua B vẽ một đường thẳng song song với \(\vec b\). Trên đườ ng thẳng đó lấy điểm C sao cho \(BC = \left| {\vec b} \right|\) và \(\overrightarrow {BC}\) cùng hướng với \({\vec b}\).
b) Ta có: \(\vec a + \vec b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Trả lời câu hỏi Hoạt động 6 trang 61 SGK Toán 12 Cánh diều
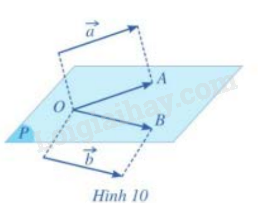
Trong không gian, cho hai vecto \(\vec a,\vec b\)khác \(\;\vec 0\). Lấy một điểm O tùy ý.
a) Vẽ hai vecto \(\overrightarrow {OA} = \vec a,\;\overrightarrow {OB} = \vec b\)
b) Khi đó , hai vecto \(\overrightarrow {OA}, \overrightarrow {OB} \) có giá nằm trong cùng mặt phẳng (P) (hình 10). Nếu định nghĩa góc giữa hai vecto \(\overrightarrow {OA}, \;\overrightarrow {OB} \) trong hai mặt phẳng (P).
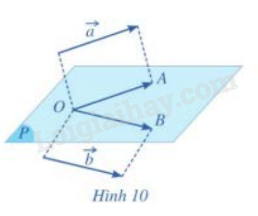
Lời giải chi tiết:
Trong không gian, cho hai vecto \(\vec a, \vec b\) khác \(\;\vec 0\). Lấy một điểm O tùy ý và vẽ hai vecto\(\;\overrightarrow {OA} = \vec a,\overrightarrow {OB} = \vec b\). Góc giữa hai vecto \(\vec a,\overrightarrow {b\;} \) trong không gian, ký hiệu \(\left( {\vec a,\vec b} \right)\) là góc giữa hai vecto \(\;\overrightarrow {OA} ,\overrightarrow {OB} \).
Trả lời câu hỏi Hoạt động 2 trang 58 SGK Toán 12 Cánh diều
Trong không gian, cho 2 vec tơ \(\vec a\) và \(\vec b\). Lấy một điểm A tùy ý.
a) Vẽ \(\overrightarrow {AB} \)\( = \vec a\),\(\overrightarrow {BC} \)\( = \vec b\)
b) Tổng của 2 vec tơ \(\vec a\)và\(\vec b\) bằng vec tơ nào trong hình 4?
Phương pháp giải:
a) Ghi rõ các bước để vẽ hình
b) Áp dụng quy tắc 3 điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
a)
– Qua A vẽ một đường thẳng song song với \(\vec a\). Trên đường thẳng đó lấy điểm B sao cho \(AB = \left| {\vec a} \right|\) và \(\overrightarrow {AB}\) cùng hướng với \({\vec a}\).
– Qua B vẽ một đường thẳng song song với \(\vec b\). Trên đườ ng thẳng đó lấy điểm C sao cho \(BC = \left| {\vec b} \right|\) và \(\overrightarrow {BC}\) cùng hướng với \({\vec b}\).
b) Ta có: \(\vec a + \vec b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Trả lời câu hỏi Hoạt động 3 trang 59 SGK Toán 12 Cánh diều
Cho hình hộp ABCD.A’B’C’D’. Tìm liên hệ giữa \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} ;\;\overrightarrow {AC} + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \).
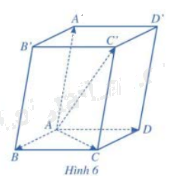
Phương pháp giải:
Áp dụng quy tắc ba điểm.
Lời giải chi tiết:
Áp dụng quy tắc ba điểm ta thấy:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {BD} \) (1)
Mà từ hình vẽ ta thấy \(\overrightarrow {BD} = \overrightarrow {AC} \;\;\;\;\;\;\;\;\left( 2 \right)\)
Từ (1) (2) => \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {A'C} \) (3)
Mà \(\overrightarrow {A'C} = \overrightarrow {AC'} \) (4)
Từ (3), (4) suy ra \(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Trả lời câu hỏi Hoạt động 4 trang 59 SGK Toán 12 Cánh diều
Trong không gian , cho hai vecto\(\;\vec a,\vec b.\;\) Lấy một điểm M tùy ý.
a) Vẽ \(\overrightarrow {MA} = \vec a,\;\overrightarrow {MB} = \vec b\;,\overrightarrow {MC} = \overrightarrow { - b} \).
b) Tổng của hai vecto \(\vec a\;\)và \(\;\overrightarrow { - b} \) bằng vecto nào trong hình 7.
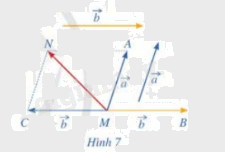
Phương pháp giải:
Sử dụng quy tắc hình bình hành.
Lời giải chi tiết:
\( \vec{a}\) + (\( - \vec{b}) =\) \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MN} \) (quy tắc hình bình hành).
Trả lời câu hỏi Hoạt động 5 trang 60 SGK Toán 12 Cánh diều
Nêu định nghĩa tích của một số thực \(k \ne 0\;\)với vecto\(\;\vec a\; \ne \vec 0\) trong mặt phẳng.
Lời giải chi tiết:
Cho số thực \(k \ne 0\) và \(vecto\;\vec a \ne \vec 0\). Tích của số k với vecto \(\vec a\) là một vecto, kí hiệu là \(k\vec a,\;\)được xác định như sau:
- Cùng hướng với vecto \(\vec a\) nếu k > 0, ngược hướng với vecto \(\vec a\) nếu k < 0.
- Có độ dài bằng \(\left| k \right|.\left| {\vec a} \right|\).
Trả lời câu hỏi Hoạt động 6 trang 61 SGK Toán 12 Cánh diều
Trong không gian, cho hai vecto \(\vec a,\vec b\)khác \(\;\vec 0\). Lấy một điểm O tùy ý.
a) Vẽ hai vecto \(\overrightarrow {OA} = \vec a,\;\overrightarrow {OB} = \vec b\)
b) Khi đó , hai vecto \(\overrightarrow {OA}, \overrightarrow {OB} \) có giá nằm trong cùng mặt phẳng (P) (hình 10). Nếu định nghĩa góc giữa hai vecto \(\overrightarrow {OA}, \;\overrightarrow {OB} \) trong hai mặt phẳng (P).
Lời giải chi tiết:
Trong không gian, cho hai vecto \(\vec a, \vec b\) khác \(\;\vec 0\). Lấy một điểm O tùy ý và vẽ hai vecto\(\;\overrightarrow {OA} = \vec a,\overrightarrow {OB} = \vec b\). Góc giữa hai vecto \(\vec a,\overrightarrow {b\;} \) trong không gian, ký hiệu \(\left( {\vec a,\vec b} \right)\) là góc giữa hai vecto \(\;\overrightarrow {OA} ,\overrightarrow {OB} \).
Trả lời câu hỏi Hoạt động 7 trang 61 SGK Toán 12 Cánh diều
Trong không gian, cho hình lập phương ABCD.A’B’C’D’ có độ dài bằng 3cm (hình 12).
a) Tính góc giữa hai vecto \(\overrightarrow {AC} ,\overrightarrow {A'D'} \).
b) Tính \(\left| {\overrightarrow {AC} } \right|,\left| {\overrightarrow {A'D'} } \right|\). Cos(\(\overrightarrow {AC} ,\overrightarrow {A'D'} \)).
Phương pháp giải:
Áp dụng quy tắc 3 điểm và vectơ trong không gian.
Lời giải chi tiết:
Ta có A’D’//AD.
Góc giữa \(\overrightarrow {AC} \;\)và\(\;\overrightarrow {A'D'} \)= \(\;\overrightarrow {AC} \) và \(\overrightarrow {AD} \).
a) Mà ABCD là hình vuông => \(\widehat {CAD} = 45^\circ \)
b) \(\overrightarrow {\left| {AC} \right|} .|\overrightarrow {A'D'|} \) = AC.AD = 3.3 = 9.
cos(\(\overrightarrow {AC} ,\overrightarrow {A'D'} \))= cos(\(\overrightarrow {AC} ,\overrightarrow {AD} )\)= \(\frac{{\overrightarrow {AC} .\overrightarrow {AD} }}{{\overrightarrow {\left| {AC} \right|} .\overrightarrow {\left| {AD} \right|} }} = \frac{{3.3}}{{3.3}} = 1\).
Mục 2 của chương trình Toán 12 tập 1 - Cánh diều tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng, đóng vai trò then chốt trong việc hiểu và giải quyết các bài toán về đạo hàm, tích phân và các ứng dụng của chúng trong các lĩnh vực khác.
Bài 1: Tính các giới hạn sau: a) lim (x→2) (x^2 - 4) / (x - 2); b) lim (x→3) (x^3 - 27) / (x - 3); c) lim (x→0) sin(x) / x.
Lời giải:
Bài 2: Cho hàm số f(x) = (x^2 - 1) / (x - 1). a) Tính f(1). b) Tính lim (x→1) f(x).
Lời giải:
Bài 3: Chứng minh rằng lim (x→0) (1 + x)^n = 1 với mọi số nguyên dương n.
Lời giải:
Sử dụng định nghĩa giới hạn và khai triển nhị thức Newton, ta có thể chứng minh được giới hạn này.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 58, 59, 60 SGK Toán 12 tập 1 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!