Chào mừng bạn đến với bài học về Lý thuyết Vecto và các phép toán vecto trong không gian, một phần quan trọng của chương trình Toán 12 Cánh Diều. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng vững chắc về vecto, các phép toán trên vecto và ứng dụng của chúng trong không gian.
Chúng tôi sẽ trình bày một cách dễ hiểu, kèm theo nhiều ví dụ minh họa và bài tập thực hành để giúp bạn nắm bắt kiến thức một cách nhanh chóng và hiệu quả.
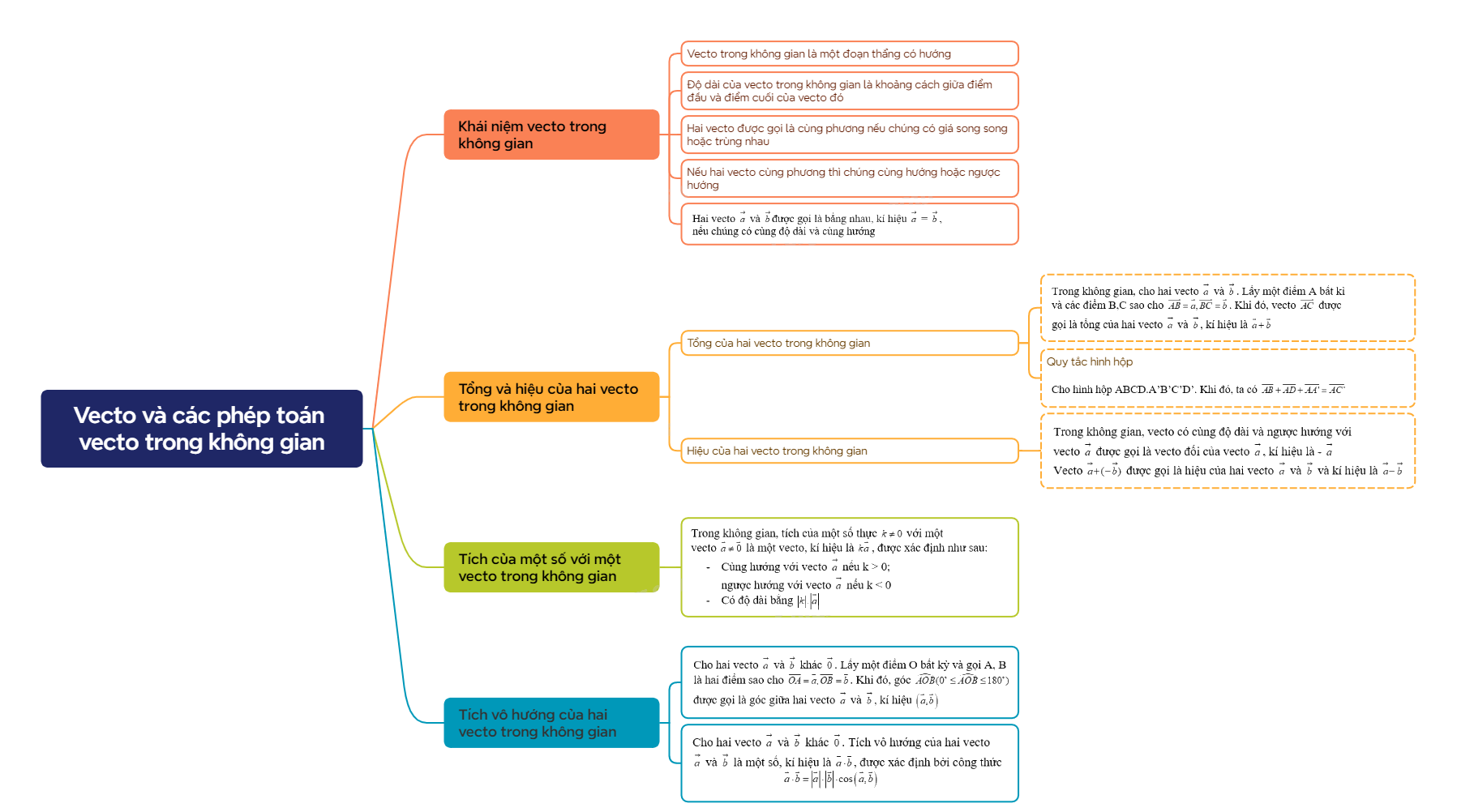
1. Khái niệm vecto trong không gian
1. Khái niệm vecto trong không gian
- Vecto trong không gian là một đoạn thẳng có hướng - Các khái niệm có liên quan đến vecto trong không gian như: giá của vecto, độ dài của vecto, vecto cùang phương, vecto cùng hướng, vecto-không, hai vecto bằng nhau, hai vecto đối nhau, … được phát biểu tương tự như trong mặt phẳng |
2. Các phép toán vecto trong không gian
a) Tổng và hiệu của hai vecto trong không gian
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Lấy một điểm A bất kì và các điểm B,C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Khi đó, vecto \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu là \(\overrightarrow a + \overrightarrow b \) - Với 3 điểm A, B, C trong không gian, ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (Quy tắc 3 điểm) - Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (Quy tắc hình bình hành) - Nếu ABCD.A’B’C’D’ là hình hộp thì \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)(Quy tắc hình hộp) |
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Hiệu của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là tổng của hai vecto \(\mathop a\limits^ \to \) và vecto đối của \(\mathop b\limits^ \to \), kí hiệu là \(\mathop a\limits^ \to - \mathop b\limits^ \to \) Với ba điểm O, A, B trong không gian, ta có: \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \) (Quy tắc hiệu) |
b) Tích của một số với một vecto trong không gian
Trong không gian, tích của một số thực \(k \ne 0\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí hiệu là \(k\overrightarrow a \), được xác định như sau: - Cùng hướng với vecto \(\mathop a\limits^ \to \) nếu k > 0; ngược hướng với vecto \(\mathop a\limits^ \to \) nếu k < 0 - Có độ dài bằng \(\left| k \right|.\left| {\overrightarrow a } \right|\) |
c) Tích vô hướng của hai vecto trong không gian
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}({0^ \circ } \le \widehat {AOB} \le {180^ \circ })\) được gọi là góc giữa hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu \(\left( {\overrightarrow a ,\overrightarrow b } \right)\) |
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Tích vô hướng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\) |
Vecto là một khái niệm cơ bản và quan trọng trong hình học không gian. Nó được sử dụng để biểu diễn hướng và độ dài của một đoạn thẳng. Trong chương trình Toán 12 Cánh Diều, việc nắm vững lý thuyết vecto và các phép toán trên vecto là điều kiện cần thiết để giải quyết các bài toán liên quan đến hình học không gian.
Một vecto được xác định bởi điểm gốc và điểm cuối. Nó có các đặc trưng sau:
Vecto thường được ký hiệu là AB, trong đó A là điểm gốc và B là điểm cuối.
Có một số phép toán cơ bản trên vecto, bao gồm:
Trong không gian, một vecto có thể được biểu diễn bằng tọa độ. Nếu A(xA, yA, zA) và B(xB, yB, zB) là hai điểm, thì AB = (xB - xA, yB - yA, zB - zA).
Khi vecto được biểu diễn bằng tọa độ, các phép toán cộng, trừ, nhân với một số thực có thể được thực hiện một cách dễ dàng:
Vecto được ứng dụng rộng rãi trong việc giải quyết các bài toán liên quan đến hình học không gian, chẳng hạn như:
Bài tập 1: Cho A(1, 2, 3) và B(4, 5, 6). Tính AB.
Giải:AB = (4 - 1, 5 - 2, 6 - 3) = (3, 3, 3).
Bài tập 2: Cho a = (1, 2, 3) và b = (4, 5, 6). Tính a + b và a - b.
Giải:a + b = (1 + 4, 2 + 5, 3 + 6) = (5, 7, 9). a - b = (1 - 4, 2 - 5, 3 - 6) = (-3, -3, -3).
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Vecto và các phép toán vecto trong không gian Toán 12 Cánh Diều. Chúc bạn học tập tốt!