Chào mừng bạn đến với bài học về lý thuyết Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trong chương trình Toán 12 Cánh Diều. Đây là một phần kiến thức quan trọng trong chương trình thống kê, giúp bạn hiểu rõ hơn về mức độ phân tán của dữ liệu.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản về phương sai, độ lệch chuẩn, cách tính toán và ứng dụng của chúng trong thực tế. Chúng tôi sẽ trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa để bạn có thể nắm bắt kiến thức một cách nhanh chóng và hiệu quả.
1. Định nghĩa
1. Định nghĩa
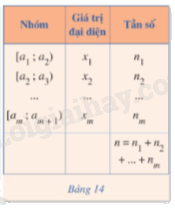
Xét mẫu số liệu ghép nhóm cho trong bảng sau:
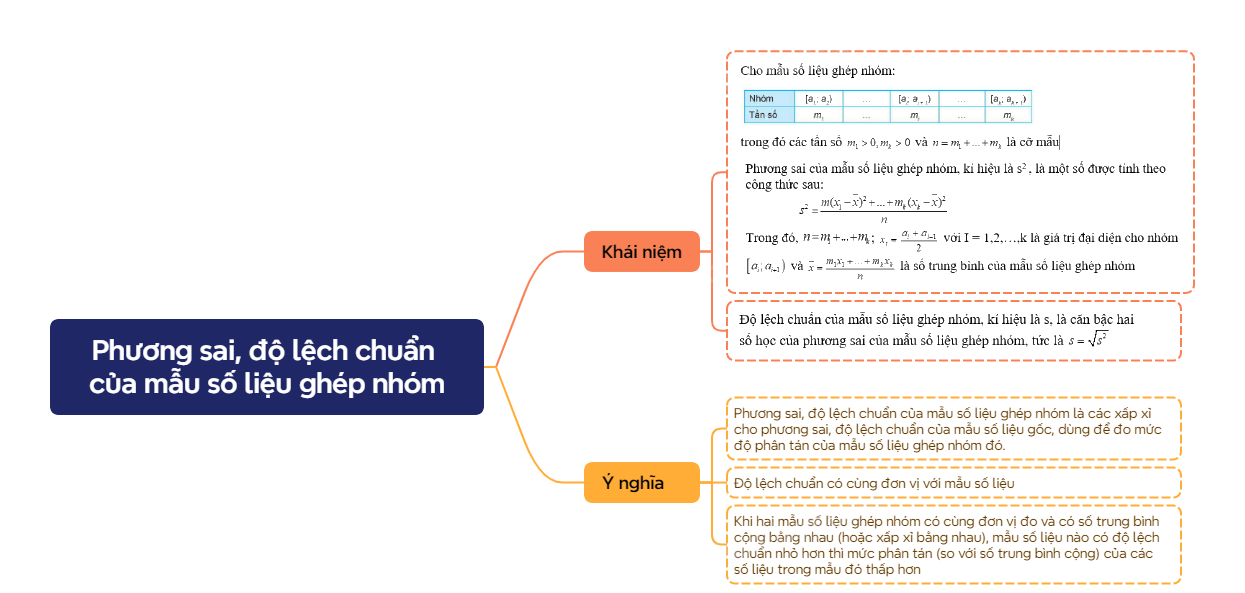
\[{s^2} = \frac{{{n_1}{{({x_1} - \overline x )}^2} + ... + {n_m}{{({x_m} - \overline x )}^2}}}{n}\] được gọi là phương sai của mấu số liệu đó. Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} .\) |
2. Ý nghĩa
Ví dụ: Anh An đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh An thống kê số tiền thu được mỗi tháng trong vòng 60 ngày theo mỗi lĩnh vực có kết quả như sau:

So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực A, B. Đầu tư vào lĩnh vực nào “rủi ro” hơn?
Giải:
Chọn giá trị đại diện cho các nhóm số liệu ta có:

Số tiền trung bình thu được khi đầu tư vào các lĩnh vực A, B tương ứng là:
\(\overline {{x_A}} = \frac{1}{{60}}(5.7,5 + ... + 5.27,5) = 17,5\) (triệu đồng)
\(\overline {{x_B}} = \frac{1}{{60}}(20.7,5 + ... + 20.27,5) = 17,5\) (triệu đồng)
Như vậy, về trung bình đầu tư vào các lĩnh vực A, B số tiền thu được hàng tháng như nhau.
Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực A, B tương ứng là:
\({s_A} = \sqrt {\frac{1}{{60}}(5.7,{5^2} + ... + 5.27,{5^2} - 17,{5^2}} = 5\)
\({s_B} = \sqrt {\frac{1}{{60}}(20.7,{5^2} + ... + 20.27,{5^2} - 17,{5^2}} \approx 8,42.\)
Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực B cao hơn khi đầu tư vào lĩnh vực A. Người ta nói rằng, đầu tư vào lĩnh vực B là “rủi ro” hơn.
Trong chương trình Toán 12, phần thống kê và xác suất đóng vai trò quan trọng, và việc hiểu rõ về phương sai, độ lệch chuẩn là nền tảng để giải quyết các bài toán liên quan đến sự phân tán của dữ liệu. Bài viết này sẽ đi sâu vào lý thuyết Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm, theo chương trình Cánh Diều, cung cấp kiến thức chi tiết, dễ hiểu và các ví dụ minh họa.
Mẫu số liệu ghép nhóm là một tập hợp các dữ liệu được chia thành các khoảng hoặc lớp, mỗi lớp chứa một số lượng quan sát nhất định. Thay vì liệt kê tất cả các giá trị riêng lẻ, chúng ta chỉ quan tâm đến tần số của mỗi lớp. Ví dụ, một bảng tần số thể hiện số lượng học sinh đạt điểm trong các khoảng điểm khác nhau là một mẫu số liệu ghép nhóm.
Phương sai (Variance) là một đại lượng đo lường mức độ phân tán của dữ liệu xung quanh giá trị trung bình. Đối với mẫu số liệu ghép nhóm, công thức tính phương sai được điều chỉnh để phù hợp với cấu trúc dữ liệu này.
Công thức tính phương sai (S2) của mẫu số liệu ghép nhóm:
S2 = ∑[(xi - x̄)2 * fi] / (n - 1)
Trong đó:
Độ lệch chuẩn (Standard Deviation) là căn bậc hai của phương sai. Nó cũng đo lường mức độ phân tán của dữ liệu, nhưng có đơn vị giống với dữ liệu gốc, giúp dễ dàng diễn giải hơn.
Công thức tính độ lệch chuẩn (S) của mẫu số liệu ghép nhóm:
S = √S2 = √[∑[(xi - x̄)2 * fi] / (n - 1)]
Giả sử chúng ta có bảng tần số sau về điểm thi Toán của một lớp học:
| Khoảng điểm | Tần số (fi) |
|---|---|
| 5 - 6 | 5 |
| 6 - 7 | 10 |
| 7 - 8 | 15 |
| 8 - 9 | 8 |
| 9 - 10 | 2 |
| Tổng | 40 |
Giá trị đại diện của mỗi khoảng điểm là trung điểm của khoảng đó: 5.5, 6.5, 7.5, 8.5, 9.5.
Áp dụng các bước tính toán như trên, ta sẽ tìm được phương sai và độ lệch chuẩn của mẫu số liệu này.
Phương sai và độ lệch chuẩn có nhiều ứng dụng trong thực tế, bao gồm:
Khi tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm, việc chọn giá trị đại diện cho mỗi lớp là rất quan trọng. Thông thường, chúng ta sử dụng trung điểm của lớp, nhưng trong một số trường hợp, có thể sử dụng các phương pháp khác để ước lượng giá trị đại diện một cách chính xác hơn.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về lý thuyết Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm Toán 12 Cánh Diều. Chúc bạn học tập tốt!