Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 86,87 SGK Toán 12 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài viết này sẽ trình bày đầy đủ các bước giải, phân tích từng khía cạnh của bài toán, đảm bảo các em hiểu rõ bản chất và áp dụng linh hoạt vào các bài tập tương tự.
Khoảng tứ phân vị
Đề bài
Trả lời câu hỏi Hoạt động 2 trang 86 SGK Toán 12 Cánh diều
Xét mẫu số liệu ghép nhóm cho bởi Bảng 5.
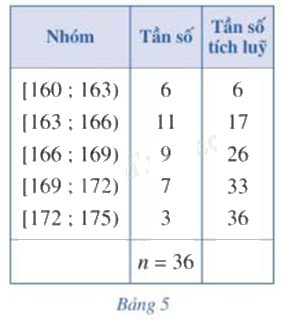
a) Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{36}}{4} = 9\) có đúng không?
Tìm đầu mút trái s, độ dài h, tần số \({n_2}\) của nhóm 2; tần số tích lũy của nhóm 1. Sau đó, hãy tính tứ phân vị thứ nhất của mẫu số liệu đã cho theo công thức sau: \({Q_1} = s + \left( {\frac{{9 - c{f_1}}}{{{n_2}}}} \right).h\)
b) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{2} = \frac{{36}}{2} = 18\) có đúng không?
Tìm đầu mút trái r, độ dài d, tần số của nhóm 3; tần số tích lũy của nhóm 2. Sau đó, hãy tính tứ phân vị thứ hai của mẫu số liệu đã cho theo công thức sau: \({Q_2} = r + \left( {\frac{{18 - c{f_2}}}{{{n_3}}}} \right).d\)
c) Nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.36}}{4} = 27\) có đúng không?
Tìm đầu mút trái t, độ dài l, tần số của nhóm 4; tần số tích lũy của nhóm 3. Sau đó, hãy tính tứ phân vị thứ ba của mẫu số liệu đã cho theo công thức sau:\({Q_3} = t + \left( {\frac{{27 - c{f_3}}}{{{n_4}}}} \right).l\)
d) Tìm hiệu \({Q_3} - {Q_1}\)
Phương pháp giải - Xem chi tiết
Quan sát bảng số liệu
Lời giải chi tiết
a) Đúng vì tần số tích lũy của nhóm 2 là 17 > 9
s = 163; h = 166 – 163 = 3; \({n_2} = 11\); \(c{f_1} = 6\)
\({Q_1} = s + \left( {\frac{{9 - c{f_1}}}{{{n_2}}}} \right).h = 163 + \left( {\frac{{9 - 6}}{{11}}} \right).3 = \frac{{1802}}{{11}}\)
b) Đúng vì tần số tích lũy của nhóm 3 là 26 > 18
r = 166; d = 169 – 166 = 3; \({n_3} = 9\); \(c{f_2} = 17\)
\({Q_2} = r + \left( {\frac{{18 - c{f_2}}}{{{n_3}}}} \right).d = 166 + \left( {\frac{{18 - 17}}{9}} \right).3 = \frac{{499}}{3}\)
c) Đúng vì tần số tích lũy của nhóm 4 là 33 > 27
t = 169; l = 172 – 169 = 3; \({n_4} = 7\); \(c{f_3} = 26\)
\({Q_3} = t + \left( {\frac{{27 - c{f_3}}}{{{n_4}}}} \right).l = 169 + \left( {\frac{{27 - 26}}{7}} \right).3 = \frac{{1186}}{7}\)
d) \({Q_3} - {Q_1} = \frac{{1186}}{7} - \frac{{1802}}{{11}} = \frac{{432}}{{77}}\)
Mục 2 của SGK Toán 12 tập 1 - Cánh diều tập trung vào việc nghiên cứu về đạo hàm của hàm số. Đây là một phần kiến thức nền tảng và quan trọng trong chương trình Toán 12, đóng vai trò then chốt trong việc giải quyết các bài toán liên quan đến cực trị, đơn điệu và ứng dụng của đạo hàm.
Mục 2 bao gồm các nội dung chính sau:
a) y = x3 - 2x2 + 5x - 1
Lời giải: y' = 3x2 - 4x + 5
b) y = sin(2x) + cos(x)
Lời giải: y' = 2cos(2x) - sin(x)
Lời giải:
Sử dụng quy tắc đạo hàm của thương:
y' = [(x2 + 1)'(x - 1) - (x2 + 1)(x - 1)'] / (x - 1)2
y' = [2x(x - 1) - (x2 + 1)] / (x - 1)2
y' = (2x2 - 2x - x2 - 1) / (x - 1)2
y' = (x2 - 2x - 1) / (x - 1)2
Lời giải:
Tính đạo hàm bậc nhất: y' = 4x3 - 8x
Giải phương trình y' = 0: 4x3 - 8x = 0 => 4x(x2 - 2) = 0 => x = 0, x = √2, x = -√2
Tính đạo hàm bậc hai: y'' = 12x2 - 8
Xét dấu y'' tại các điểm cực trị:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên, các em học sinh đã hiểu rõ cách giải các bài tập mục 2 trang 86,87 SGK Toán 12 tập 1 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!