Chào mừng bạn đến với bài học về lý thuyết Tính đơn điệu của hàm số trong chương trình Toán 12 Cánh Diều.
Đây là một trong những chủ đề quan trọng giúp bạn hiểu sâu hơn về tính chất của hàm số và ứng dụng của đạo hàm.
Chúng tôi sẽ cung cấp lý thuyết đầy đủ, ví dụ minh họa và bài tập thực hành để bạn có thể nắm vững kiến thức này.
1.Nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm
1.Nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm
Định lý 1
Cho hàm số y = f(x) có đạo hàm trên tập \(K \subset R\), trong đó K là một khoảng, đoạn hoặc nửa khoảng - Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K - Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K |
Ví dụ: Hàm số y = |x| đồng biến trên khoảng \(\left( {0; + \infty } \right)\), nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\)
Định lý 2
Cho hàm số y = f(x) có đạo hàm trên tập \(K \subset R\), trong đó K là một khoảng, đoạn hoặc nửa khoảng. Nếu f’(x) \( \ge \) 0 (hoặc f’(x) \( \le \) 0) với mọi x thuộc K và f’(x) = 0 chỉ tại một số hữa hạn điểm của K thì hàm số f(x) đồng biến (hoặc nghịch biến) trên K |
Ví dụ: Hàm số \(y = {x^2} - 4x + 2\) có y’ = 2x – 4
y’ > 0 với \(x \in (2; + \infty )\) nên HS đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
y’ < 0 với \(x \in ( - \infty ;2)\) nên HS đồng biến trên khoảng \(\left( { - \infty ;2} \right)\)
2. Điểm cực trị, giá trị cực trị của hàm số
Khái niệm cực trị của hàm số
Cho hàm số y = f(x) liên tục trên tập \(K \subset R\), trong đó K là một khoảng, đoạn hoặc nửa khoảng và \({x_0} \in K,{x_1} \in K\) - \({x_0}\) được gọi là một điểm cực đại của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm \({x_0}\) sao cho (a;b) \( \subset \) K và \(f(x) < f({x_0})\) với mọi \(x \in (a;b)\) và \(x \ne {x_0}\). Khi đó, \(f({x_0})\) được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là - \({x_1}\) được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm \({x_0}\) sao cho (c;d) \( \subset \) K và \(f(x) > f({x_1})\) với mọi \(x \in (c;d)\) và \(x \ne {x_1}\). Khi đó, \(f({x_1})\) được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là \({f_{CT}}\) Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị) |
Ví dụ: Cho đồ thị của hàm số y = f(x) như sau
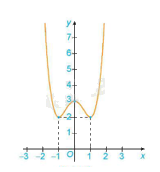
Hàm số đạt cực tiểu tại x = -1 và \({y_{CT}}\)= y(-1) = 2
Hàm số đạt cực đại tại x = 0 và = y(0) = 3
Hàm số đạt cực tiểu tại x = 1 và \({y_{CT}}\)= y(1) = 2
Định lý
Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó: a) Nếu f’(x) < 0 với mọi \(x \in \left( {a;{x_0}} \right)\) và f’(x) > 0 với mọi \(x \in \left( {{x_0};b} \right)\) thì hàm số f(x) đạt cực tiểu tại điểm \({x_0}\) b) Nếu f’(x) > 0 với mọi \(x \in \left( {a;{x_0}} \right)\) và f’(x) < 0 với mọi \(x \in \left( {{x_0};b} \right)\) thì hàm số f(x) đạt cực tiểu tại điểm \({x_0}\) |
Ví dụ: Tìm cực trị của hàm số \(y = {x^3} - 6{x^2} + 9x + 30\).
Tập xác định của hàm số là R.
Ta có: \(y' = 3{x^2} - 12x + 9\); y’ = 0 \( \Leftrightarrow \)x = 1 hoặc x = 3.
BBT:
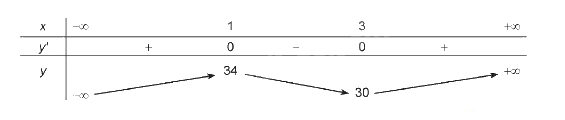
Hàm số đạt cực đại tại x = 1 và = y(1) = 34
Hàm số đạt cực tiểu tại x = 3 và \({y_{CT}}\)= y(3) = 30
Tính đơn điệu của hàm số là một khái niệm quan trọng trong chương trình Toán 12, đặc biệt là khi học về đạo hàm và ứng dụng của đạo hàm. Hiểu rõ lý thuyết này giúp học sinh phân tích và dự đoán được sự thay đổi của hàm số trên các khoảng khác nhau, từ đó giải quyết các bài toán liên quan một cách hiệu quả.
Một hàm số f được gọi là đồng biến trên một khoảng I nếu với mọi x1, x2 thuộc I, sao cho x1 < x2 thì f(x1) ≤ f(x2). Hàm số được gọi là nghịch biến trên một khoảng I nếu với mọi x1, x2 thuộc I, sao cho x1 < x2 thì f(x1) ≥ f(x2).
Giả sử hàm số f liên tục trên khoảng I và có đạo hàm trên khoảng đó.
Xét hàm số f(x) = x3 - 3x2 + 2.
f'(x) = 3x2 - 6x = 3x(x - 2).
Giải phương trình f'(x) = 0, ta được x = 0 và x = 2.
Lập bảng xét dấu f'(x):
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Vậy hàm số f(x) đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Tính đơn điệu của hàm số có nhiều ứng dụng trong việc giải các bài toán liên quan đến cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số, và các bài toán thực tế khác. Việc nắm vững lý thuyết và kỹ năng xét tính đơn điệu là nền tảng quan trọng để giải quyết các bài toán này một cách hiệu quả.
Khi xét tính đơn điệu của hàm số, cần chú ý đến tập xác định của hàm số và các điểm không xác định của đạo hàm. Ngoài ra, cần kiểm tra kỹ các điều kiện để đảm bảo tính đúng đắn của kết quả.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Tính đơn điệu của hàm số Toán 12 Cánh Diều. Chúc bạn học tập tốt!