Chào mừng các em học sinh đến với lời giải chi tiết bài tập 8 trang 27 SGK Toán 12 tập 2 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập 8 thuộc chương trình học Toán 12 tập 2, tập trung vào các kiến thức về tích phân.
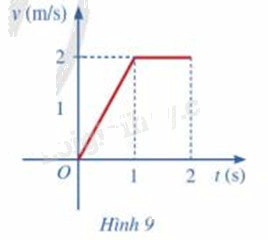
Một vật chuyển động với vận tốc được cho bởi đồ thị ở Hình 9. a) Tính quãng đường mà vật di chuyển được trong 1 giây đầu tiên b) Tính quãng đường mà vật di chuyển được trong 2 giây đầu tiên
Đề bài
Một vật chuyển động với vận tốc được cho bởi đồ thị ở Hình 9.
a) Tính quãng đường mà vật di chuyển được trong 1 giây đầu tiên
b) Tính quãng đường mà vật di chuyển được trong 2 giây đầu tiên
Phương pháp giải - Xem chi tiết
Xác định vận tốc ở các khoảng thời gian và tính toán quãng đường thông qua tích phân
Lời giải chi tiết
a) Trong 1 giây đầu tiên, vận tốc được biểu diễn bởi hàm số: \(v(t) = 2t\)
Quãng đường mà vật di chuyển được trong 1 giây đầu tiên: \(s(1) = \int\limits_0^1 {v(t)} dt = \int\limits_0^1 {2t} dt = 1\) (m)
b) Trong 1 giây tiếp theo, \(v = 2(m/s)\)
Quãng đường mà vật di chuyển được trong 2 giây đầu tiên: \(s(2) = \int\limits_0^1 {v(t)} dt + \int\limits_1^2 {v(t)} dt = \int\limits_0^1 {2t} dt + \int\limits_0^1 2 dt = 3\) (m)
Bài tập 8 trang 27 SGK Toán 12 tập 2 - Cánh diều yêu cầu học sinh vận dụng kiến thức về tích phân để tính diện tích hình phẳng giới hạn bởi các đường cong. Đây là một dạng bài tập quan trọng, thường xuyên xuất hiện trong các kỳ thi THPT Quốc gia. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về tích phân, phương pháp tính tích phân và các kỹ năng vẽ đồ thị hàm số.
Bài tập 8 bao gồm các câu hỏi nhỏ, yêu cầu học sinh tính diện tích các hình phẳng khác nhau. Cụ thể:
Để giải bài tập 8, học sinh có thể áp dụng các phương pháp sau:
Lời giải:
Đầu tiên, ta tìm giao điểm của đường cong y = x2 - 4x + 3 với trục hoành:
x2 - 4x + 3 = 0 ⇔ (x - 1)(x - 3) = 0 ⇔ x = 1 hoặc x = 3
Vậy, đường cong cắt trục hoành tại x = 1 và x = 3. Trên đoạn [0, 1], y > 0 và trên đoạn [1, 3], y < 0.
Diện tích hình phẳng cần tính là:
S = ∫01 (x2 - 4x + 3) dx + |∫13 (x2 - 4x + 3) dx|
Tính các tích phân:
∫01 (x2 - 4x + 3) dx = [x3/3 - 2x2 + 3x]01 = 1/3 - 2 + 3 = 4/3
∫13 (x2 - 4x + 3) dx = [x3/3 - 2x2 + 3x]13 = (9 - 18 + 9) - (1/3 - 2 + 3) = 0 - 4/3 = -4/3
Vậy, S = 4/3 + |-4/3| = 4/3 + 4/3 = 8/3
Lời giải:
Trên đoạn [0, π], sinx ≥ 0. Vậy, diện tích hình phẳng cần tính là:
S = ∫0π sinx dx = [-cosx]0π = -cosπ - (-cos0) = -(-1) - (-1) = 1 + 1 = 2
Lời giải:
Trên đoạn [-1, 1], ex > 0. Vậy, diện tích hình phẳng cần tính là:
S = ∫-11 ex dx = [ex]-11 = e1 - e-1 = e - 1/e
Bài tập 8 trang 27 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng, giúp học sinh rèn luyện kỹ năng tính tích phân và ứng dụng vào việc tính diện tích hình phẳng. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.