Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết bài tập 1 trang 88 SGK Toán 12 tập 1 - Cánh diều. Mục tiêu của chúng ta là nắm vững kiến thức và kỹ năng giải toán, từ đó đạt kết quả tốt nhất trong các kỳ thi.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, chúng tôi cam kết mang đến cho các em những bài giải chất lượng và dễ hiểu nhất.
Bảng 8 biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: A. 50 B. 30 C. 6 D. 69,8 b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: A. 50 B. 40 C. 14,23 D. 70,87
Đề bài
Bảng 8 biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày
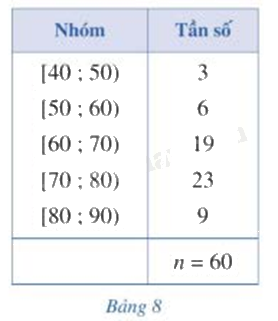
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
A. 50
B. 30
C. 6
D. 69,8
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:
A. 50
B. 40
C. 14,23
D. 70,87
Phương pháp giải - Xem chi tiết
a) Khoảng biến thiên là hiệu của đầu mút phải nhóm cuối cùng và đầu mút trái nhóm đầu tiên
b) Khoảng tứ phân vị là \({Q_3} - {Q_1}\)
Lời giải chi tiết
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: \(R = 90 - 40 = 50\)
Chọn A
b) Số phần tử của mẫu là n = 42
Tần số tích lũy của các nhóm lần lượt là \(c{f_1} = 3\), \(c{f_2} = 9\), \(c{f_3} = 28\), \(c{f_4} = 51\), \(c{f_5} = 60\)
Ta có: \(\frac{n}{4} = \frac{{60}}{4} = 15\) mà 9 < 15 < 28 suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 15. Xét nhóm 3 là nhóm [60;70] có s = 60, h = 10, \({n_3} = 19\)và nhóm 2 là nhóm [50;60] có \(c{f_2} = 9\)
Ta có tứ phân vị thứ nhất là: \({Q_1} = s + \left( {\frac{{15 - c{f_2}}}{{{n_3}}}} \right).h = 60 + \left( {\frac{{15 - 9}}{{19}}} \right).10 = \frac{{1200}}{{19}}\)
Ta có: \(\frac{{3n}}{4} = \frac{{3.60}}{4} = 45\) mà 28 < 45 < 51 suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 45. Xét nhóm 4 là nhóm [70;80] có t = 70, l = 10, \({n_4} = 23\)và nhóm 3 là nhóm [60;70] có \(c{f_3} = 28\)
Ta có tứ phân vị thứ ba là: \({Q_3} = t + \left( {\frac{{45 - c{f_3}}}{{{n_4}}}} \right).l = 70 + \left( {\frac{{45 - 28}}{{23}}} \right).10 = \frac{{1780}}{{23}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: \({Q_3} - {Q_1} = \frac{{1780}}{{23}} - \frac{{1200}}{{19}} \approx 14,23\)
Chọn C
Bài tập 1 trang 88 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về giới hạn của hàm số. Đây là một phần kiến thức quan trọng, nền tảng cho việc học các chương trình Toán học nâng cao hơn. Bài tập này yêu cầu học sinh vận dụng các định nghĩa và tính chất của giới hạn để giải quyết các bài toán cụ thể.
Bài tập 1 bao gồm các câu hỏi trắc nghiệm và bài tập tự luận. Các câu hỏi trắc nghiệm thường kiểm tra khả năng hiểu và vận dụng các khái niệm cơ bản về giới hạn. Các bài tập tự luận yêu cầu học sinh chứng minh các giới hạn hoặc tìm giới hạn của các hàm số phức tạp hơn.
Để giải quyết bài tập 1 trang 88 SGK Toán 12 tập 1 - Cánh diều một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 1 trang 88 SGK Toán 12 tập 1 - Cánh diều:
Đề bài: Tính lim (2x + 1) khi x -> 2.
Lời giải:
Áp dụng tính chất giới hạn của tổng, ta có:
lim (2x + 1) = lim 2x + lim 1 = 2 * lim x + 1 = 2 * 2 + 1 = 5.
Đáp án: 5
Đề bài: Tính lim (x^2 - 4) / (x - 2) khi x -> 2.
Lời giải:
Ta có thể phân tích tử thức thành nhân tử:
x^2 - 4 = (x - 2)(x + 2)
Do đó:
lim (x^2 - 4) / (x - 2) = lim (x - 2)(x + 2) / (x - 2) = lim (x + 2) = 2 + 2 = 4.
Đáp án: 4
Giaitoan.edu.vn cung cấp đầy đủ các bài giải SGK Toán 12 tập 1, tập 2, cùng với các bài tập trắc nghiệm và tài liệu ôn thi hữu ích. Chúng tôi luôn cập nhật nội dung mới nhất và đảm bảo chất lượng của các bài giải. Hãy truy cập giaitoan.edu.vn để học Toán hiệu quả hơn!
| Công thức | Mô tả |
|---|---|
| lim c = c | Giới hạn của một hằng số bằng chính hằng số đó. |
| lim x = a | Giới hạn của x khi x tiến tới a bằng a. |
| lim (f(x) + g(x)) = lim f(x) + lim g(x) | Giới hạn của tổng bằng tổng các giới hạn. |
| lim (f(x) * g(x)) = lim f(x) * lim g(x) | Giới hạn của tích bằng tích các giới hạn. |