Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 12 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong môn Toán.
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra. Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?
Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cánh diều
Hãy giải bài toán mở đầu bằng cách lập bảng thống kê như trong Ví dụ 2, biết rằng cả hai nhà máy sản xuất được 10 000 linh kiện.
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra.
Phương pháp giải:
Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
Số linh kiện do nhà máy I sản xuất là: \(10\;000.55\% = 5\;500\) (linh kiện).
Số linh kiện do nhà máy II sản xuất là: \(10\;000.45\% = 4\;500\) (linh kiện).
Số linh do nhà máy I sản xuất đạt tiêu chuẩn là:
\(5\;500.90\% = 4\;950\) (linh kiện).
Số linh do nhà máy I sản xuất không đạt tiêu chuẩn là: \(5\;500 - 4\;950 = 550\) (linh kiện).
Số linh do nhà máy II sản xuất đạt tiêu chuẩn là: \(4\;500.87\% = 3\;915\) (linh kiện).
Số linh do nhà máy II sản xuất không đạt tiêu chuẩn là: \(4\;500 - 3\;915 = 585\) (linh kiện).
Ta có bảng thống kê như sau:
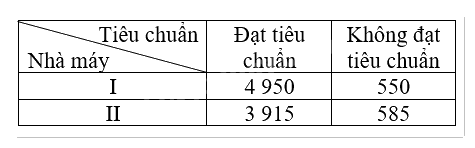
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\).
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
Trả lời câu hỏi Hoạt động 1 trang 97 SGK Toán 12 Cánh diều
Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
a) Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, \(A \cap B,A \cap \overline B \) (Hình 2).
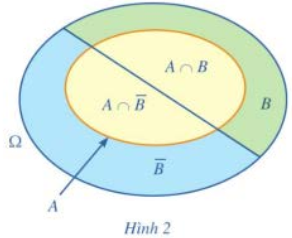
b) So sánh n(A) và \(n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\). Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\).
c) So sánh \(P\left( {A \cap B} \right)\) và \(P\left( B \right).P\left( {A|B} \right)\);
\(P\left( {A \cap \overline B } \right)\) và \(P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Phương pháp giải:
+ Sử dụng kiến thức về định nghĩa xác suất có điều kiện để tính: Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, kí hiệu là P(A|B). Nếu \(P\left( B \right) > 0\) thì \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\).
+ Sử dụng kiến thức về công thức tính xác suất của hai biến cố xung khắc: Nếu A và B là hai biến cố xung khắc thì \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
Lời giải chi tiết:
a) \(A = \left\{ {3;{\rm{ }}6;{\rm{ }}9;{\rm{ }}12;{\rm{ }}15;{\rm{ }}18;{\rm{ }}21;{\rm{ }}24} \right\},B = \left\{ {4;{\rm{ }}8;{\rm{ }}12;{\rm{ }}16;{\rm{ }}20;{\rm{ }}24} \right\}\), \(\Omega = \left\{ {1;2;3;...;24} \right\}\)\(A \cap B = \left\{ {12;24} \right\},A \cap \overline B = \left\{ {3;6;9;15;18;21} \right\}\).
b) Ta có: \(n\left( A \right) = 8,n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right) = 2 + 6 = 8\) nên \(n\left( A \right) = n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\).
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)}}{{n\left( \Omega \right)}} = \frac{{n\left( {A \cap B} \right)}}{{n\left( \Omega \right)}} + \frac{{n\left( {A \cap \overline B } \right)}}{{n\left( \Omega \right)}} = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\)
c) Ta có: \(P\left( B \right).P\left( {A|B} \right) = P\left( B \right).\frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = P\left( {A \cap B} \right)\);
\(P\left( {\overline B } \right).P\left( {A|\overline B } \right) = P\left( {\overline B } \right).\frac{{P\left( {A \cap \overline B } \right)}}{{P\left( {\overline B } \right)}} = P\left( {A \cap \overline B } \right)\).
Vì \(A \cap B,A \cap \overline B \) là hai biến cố xung khắc nên \(\left( {A \cap B} \right) \cup \left( {A \cap \overline B } \right) = A\), theo công thức xác suất ta có: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Trả lời câu hỏi Luyện tập 2 trang 100 SGK Toán 12 Cánh diều
Hãy giải bài toán mở đầu bằng phương pháp sử dụng sơ đồ hình cây như trong Ví dụ 3.
Phương pháp giải:
+ Sử dụng kiến thức sơ đồ hình cây để tính.
+ Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {B|A} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\)
Sơ đồ hình cây biểu thị tình huống đã cho:
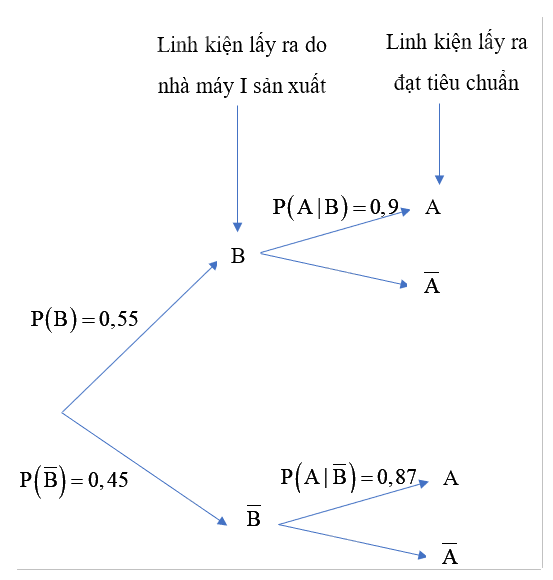 p
p
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {B|A} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
Trả lời câu hỏi Bài toán mở đầu trang 97 SGK Toán 12 Cánh diều
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra. Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?

Phương pháp giải:
Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\)
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
Trả lời câu hỏi Bài toán mở đầu trang 97 SGK Toán 12 Cánh diều
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra. Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?

Phương pháp giải:
Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\)
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
Trả lời câu hỏi Hoạt động 1 trang 97 SGK Toán 12 Cánh diều
Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
a) Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, \(A \cap B,A \cap \overline B \) (Hình 2).
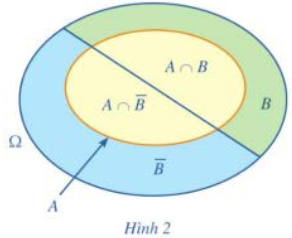
b) So sánh n(A) và \(n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\). Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\).
c) So sánh \(P\left( {A \cap B} \right)\) và \(P\left( B \right).P\left( {A|B} \right)\);
\(P\left( {A \cap \overline B } \right)\) và \(P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Phương pháp giải:
+ Sử dụng kiến thức về định nghĩa xác suất có điều kiện để tính: Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, kí hiệu là P(A|B). Nếu \(P\left( B \right) > 0\) thì \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\).
+ Sử dụng kiến thức về công thức tính xác suất của hai biến cố xung khắc: Nếu A và B là hai biến cố xung khắc thì \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
Lời giải chi tiết:
a) \(A = \left\{ {3;{\rm{ }}6;{\rm{ }}9;{\rm{ }}12;{\rm{ }}15;{\rm{ }}18;{\rm{ }}21;{\rm{ }}24} \right\},B = \left\{ {4;{\rm{ }}8;{\rm{ }}12;{\rm{ }}16;{\rm{ }}20;{\rm{ }}24} \right\}\), \(\Omega = \left\{ {1;2;3;...;24} \right\}\)\(A \cap B = \left\{ {12;24} \right\},A \cap \overline B = \left\{ {3;6;9;15;18;21} \right\}\).
b) Ta có: \(n\left( A \right) = 8,n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right) = 2 + 6 = 8\) nên \(n\left( A \right) = n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\).
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)}}{{n\left( \Omega \right)}} = \frac{{n\left( {A \cap B} \right)}}{{n\left( \Omega \right)}} + \frac{{n\left( {A \cap \overline B } \right)}}{{n\left( \Omega \right)}} = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\)
c) Ta có: \(P\left( B \right).P\left( {A|B} \right) = P\left( B \right).\frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = P\left( {A \cap B} \right)\);
\(P\left( {\overline B } \right).P\left( {A|\overline B } \right) = P\left( {\overline B } \right).\frac{{P\left( {A \cap \overline B } \right)}}{{P\left( {\overline B } \right)}} = P\left( {A \cap \overline B } \right)\).
Vì \(A \cap B,A \cap \overline B \) là hai biến cố xung khắc nên \(\left( {A \cap B} \right) \cup \left( {A \cap \overline B } \right) = A\), theo công thức xác suất ta có: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cánh diều
Hãy giải bài toán mở đầu bằng cách lập bảng thống kê như trong Ví dụ 2, biết rằng cả hai nhà máy sản xuất được 10 000 linh kiện.
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra.
Phương pháp giải:
Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
Số linh kiện do nhà máy I sản xuất là: \(10\;000.55\% = 5\;500\) (linh kiện).
Số linh kiện do nhà máy II sản xuất là: \(10\;000.45\% = 4\;500\) (linh kiện).
Số linh do nhà máy I sản xuất đạt tiêu chuẩn là:
\(5\;500.90\% = 4\;950\) (linh kiện).
Số linh do nhà máy I sản xuất không đạt tiêu chuẩn là: \(5\;500 - 4\;950 = 550\) (linh kiện).
Số linh do nhà máy II sản xuất đạt tiêu chuẩn là: \(4\;500.87\% = 3\;915\) (linh kiện).
Số linh do nhà máy II sản xuất không đạt tiêu chuẩn là: \(4\;500 - 3\;915 = 585\) (linh kiện).
Ta có bảng thống kê như sau:
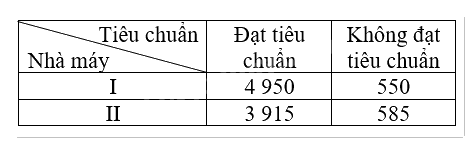
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\).
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
Trả lời câu hỏi Luyện tập 2 trang 100 SGK Toán 12 Cánh diều
Hãy giải bài toán mở đầu bằng phương pháp sử dụng sơ đồ hình cây như trong Ví dụ 3.
Phương pháp giải:
+ Sử dụng kiến thức sơ đồ hình cây để tính.
+ Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {B|A} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\)
Sơ đồ hình cây biểu thị tình huống đã cho:
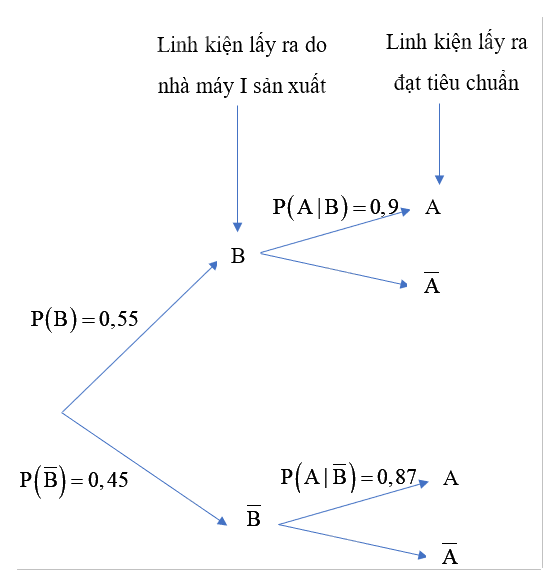 p
p
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {B|A} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
Mục 1 của SGK Toán 12 tập 2 - Cánh diều tập trung vào các kiến thức về Đạo hàm của hàm số. Đây là một phần quan trọng, nền tảng cho việc học tập các kiến thức nâng cao hơn trong chương trình Toán 12. Việc nắm vững các khái niệm, định lý và kỹ năng giải bài tập trong mục này là vô cùng cần thiết.
Để giải tốt các bài tập trong Mục 1, các em cần:
Bài 1: Tính đạo hàm của hàm số f(x) = x3 - 2x2 + 5x - 1.
Lời giải: f'(x) = 3x2 - 4x + 5.
Bài 2: Tính đạo hàm của hàm số g(x) = sin(x) + cos(x).
Lời giải: g'(x) = cos(x) - sin(x).
Bài 3: Tìm đạo hàm của hàm số h(x) = ex + ln(x).
Lời giải: h'(x) = ex + 1/x.
Bài 4: Tính đạo hàm của hàm số y = (x2 + 1)/(x - 1).
Lời giải: y' = (2x(x-1) - (x2 + 1))/(x-1)2 = (x2 - 2x - 1)/(x-1)2.
Bài 5: Cho hàm số u(x) = x2. Tính u'(x) tại x = 2.
Lời giải: u'(x) = 2x. u'(2) = 4.
Bài 6: Tìm đạo hàm của hàm số v(x) = √(x + 1).
Lời giải: v'(x) = 1/(2√(x + 1)).
Bài 7: Sử dụng đạo hàm để tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Lời giải: f'(x) = 3x2 - 6x. Giải phương trình f'(x) = 0, ta được x = 0 và x = 2. Khảo sát dấu của f'(x) để xác định cực đại, cực tiểu.
Bài 8: Khảo sát hàm số y = x4 - 4x2 + 3.
Lời giải: Tính đạo hàm bậc nhất và bậc hai, tìm các điểm cực trị, điểm uốn và vẽ đồ thị hàm số.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài toán về đạo hàm. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức.