Trả lời câu hỏi trang 52 SGK Toán 12 tập 2 - Cánh diều

Giải đáp chi tiết câu hỏi trang 52 SGK Toán 12 tập 2 - Cánh diều

Bạn đang gặp khó khăn trong việc giải các bài tập Toán 12 tập 2 trang 52 sách Cánh diều? Đừng lo lắng, giaitoan.edu.vn sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.

Chúng tôi cam kết cung cấp đáp án chính xác, phương pháp giải rõ ràng, cùng với những lưu ý quan trọng để bạn hiểu sâu sắc từng bài tập.

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm A(1;-1;2) và có vecto pháp tuyến là (overrightarrow n = (1;2;3)) Giả sử M(x;y;z) là một điểm tùy ý thuộc mặt phẳng (P) (Hình 7) a) Tính tích vô hướng (overrightarrow n .overrightarrow {AM} ) theo x, y, z b) Tọa độ (x;y;z) của điểm M có thỏa mãn phương trình: x + 2y + 3z – 5 = 0 hay không?

Đề bài

Trả lời câu hỏi Hoạt động 4 trang 52 SGK Toán 12 Cánh diều

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm A(1;-1;2) và có vecto pháp tuyến là \(\overrightarrow n = (1;2;3)\)

Giả sử M(x;y;z) là một điểm tùy ý thuộc mặt phẳng (P) (Hình 7)

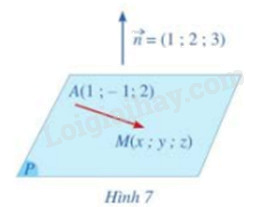
Trả lời câu hỏi trang 52 SGK Toán 12 tập 2 - Cánh diều 1

a) Tính tích vô hướng \(\overrightarrow n .\overrightarrow {AM} \) theo x, y, z

b) Tọa độ (x;y;z) của điểm M có thỏa mãn phương trình: x + 2y + 3z – 5 = 0 hay không?

Phương pháp giải - Xem chi tiết Trả lời câu hỏi trang 52 SGK Toán 12 tập 2 - Cánh diều 2

a) Sử dụng công thức biểu thức tọa độ của tích vô hướng

b) Thay tọa độ điểm M vào phương trình

Lời giải chi tiết

a) \(\overrightarrow {AM} = (x - 1;y + 1;z - 2)\)

\(\overrightarrow n .\overrightarrow {AM} = (x - 1) + 2(y + 1) + 3(z - 2) = x + 2y + 3z - 5\)

b) Tọa độ (x;y;z) của điểm M có thỏa mãn phương trình: x + 2y + 3z – 5 = 0

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Trả lời câu hỏi trang 52 SGK Toán 12 tập 2 - Cánh diều đặc sắc thuộc chuyên mục toán lớp 12 trên nền tảng toán học. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải đáp chi tiết câu hỏi trang 52 SGK Toán 12 tập 2 - Cánh diều

Trang 52 SGK Toán 12 tập 2 - Cánh diều tập trung vào các bài tập liên quan đến đạo hàm của hàm số. Đây là một phần kiến thức quan trọng, nền tảng cho việc giải quyết nhiều bài toán phức tạp hơn trong chương trình học.

Bài 1: Tính đạo hàm của các hàm số sau:

f(x) = x³ - 2x² + 5x - 1
g(x) = (x² + 1)(x - 3)
h(x) = sin(2x)

Lời giải:

f'(x) = 3x² - 4x + 5. Áp dụng quy tắc đạo hàm của tổng và đạo hàm của lũy thừa.
g'(x) = 2x(x-3) + (x² + 1) = 3x² - 6x + 1. Sử dụng quy tắc đạo hàm của tích.
h'(x) = 2cos(2x). Áp dụng quy tắc đạo hàm của hàm hợp.

Bài 2: Tìm đạo hàm của hàm số y = (x² + 2) / (x - 1)

Lời giải:

Sử dụng quy tắc đạo hàm của thương:

y' = [(2x)(x-1) - (x² + 2)(1)] / (x-1)² = (2x² - 2x - x² - 2) / (x-1)² = (x² - 2x - 2) / (x-1)²

Bài 3: Cho hàm số f(x) = x⁴ - 4x³ + 6x² - 4x + 1. Tìm f'(x) và giải phương trình f'(x) = 0.

Lời giải:

f'(x) = 4x³ - 12x² + 12x - 4. Áp dụng quy tắc đạo hàm của tổng và lũy thừa.

Giải phương trình f'(x) = 0:

4x³ - 12x² + 12x - 4 = 0

x³ - 3x² + 3x - 1 = 0

(x - 1)³ = 0

x = 1

Lưu ý quan trọng khi giải bài tập về đạo hàm:

Nắm vững các quy tắc đạo hàm cơ bản: đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
Chú ý đến các hàm số lượng giác và hàm số mũ.
Kiểm tra lại kết quả sau khi tính đạo hàm.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.

Ứng dụng của đạo hàm trong thực tế:

Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:

Tính vận tốc và gia tốc: Trong vật lý, đạo hàm của quãng đường theo thời gian là vận tốc, và đạo hàm của vận tốc theo thời gian là gia tốc.
Tìm cực trị của hàm số: Đạo hàm được sử dụng để tìm các điểm cực đại và cực tiểu của hàm số, giúp xác định giá trị lớn nhất và nhỏ nhất của hàm số trong một khoảng nhất định.
Tối ưu hóa: Đạo hàm được sử dụng để tối ưu hóa các bài toán thực tế, chẳng hạn như tối ưu hóa lợi nhuận, chi phí, hoặc hiệu suất.

Hy vọng với lời giải chi tiết và những lưu ý trên, bạn sẽ tự tin hơn khi giải các bài tập trang 52 SGK Toán 12 tập 2 - Cánh diều. Chúc bạn học tốt!