Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 2 - Cánh diều. Bài tập 10 trang 43 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các khái niệm và kỹ năng đã được học.
Chúng tôi hiểu rằng việc tự giải bài tập có thể gặp nhiều khó khăn, vì vậy chúng tôi đã biên soạn lời giải chi tiết, dễ hiểu, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Một chiếc xe ô tô chạy thử nghiệm trên một đường thẳng bắt đầu từ trạng thái đứng yên. Tốc độ của chiếc xe ô tô đó (tính bằng mét/giây) lần lượt ở giây thứ 10, thứ 20, thứ 30, thứ 40, thứ 50 và thứ 60 được ghi lại trong Bảng 1 a) Hãy xây dựng hàm số bậc ba (y = f(x) = a{x^3} + b{x^2} + cx + d(a ne 0)) để biểu diễn các số liệu ở Bảng 1, tức là ở hệ trục tọa độ Oxy, đồ thị của hàm số đó trên nửa khoảng ([0; + infty )) “gần” với các điểm O(0;0), B(10;5), C(20;21), D(30;40), E(40;62), G(50
Đề bài
Một chiếc xe ô tô chạy thử nghiệm trên một đường thẳng bắt đầu từ trạng thái đứng yên. Tốc độ của chiếc xe ô tô đó (tính bằng mét/giây) lần lượt ở giây thứ 10, thứ 20, thứ 30, thứ 40, thứ 50 và thứ 60 được ghi lại trong Bảng 1.
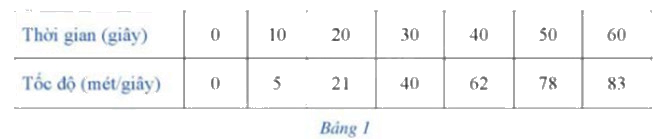
a) Hãy xây dựng hàm số bậc ba \(y = f(x) = a{x^3} + b{x^2} + cx + d(a \ne 0)\) để biểu diễn các số liệu ở Bảng 1, tức là ở hệ trục tọa độ Oxy, đồ thị của hàm số đó trên nửa khoảng \([0; + \infty )\) “gần” với các điểm O(0;0), B(10;5), C(20;21), D(30;40), E(40;62), G(50;78), K(60;83).
b) Hãy tính (gần đúng) quãng đường mà xe ô tô đó đã đi được tính đến giây thứ 60 của quá trình thử nghiệm.
Phương pháp giải - Xem chi tiết
a) Thay các giá trị vào hàm số và giải hệ phương trình.
b) Tính quãng đường thông qua tích phân của vận tốc.
Lời giải chi tiết
a) \(v(t) = a{t^3} + b{t^2} + ct + d(a \ne 0)\) với t là thời gian (giây).
Ta có:
\(\left\{ \begin{array}{l}v(0) = d = 0\\v(10) = 1000a + 100b + 10c + d = 5\\v(20) = 8000a + 400b + 20c + d = 21\\v(30) = 27000a + 900b + 30c + d = 40\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}d = 0\\a = - \frac{1}{{750}}\\b = \frac{{19}}{{200}}\\c = - \frac{{19}}{{60}}\end{array} \right.\).
Vậy \(v(t) = - \frac{1}{{750}}{t^3} + \frac{{19}}{{200}}{t^2} - \frac{{19}}{{60}}t\).
b) Quãng đường mà xe ô tô đó đã đi được tính đến giây thứ 60 của quá trình thử nghiệm là:
\(\int\limits_0^{60} {v(t)} dt = \int\limits_0^{60} {\left( { - \frac{1}{{750}}{t^3} + \frac{{19}}{{200}}{t^2} - \frac{{19}}{{60}}t} \right)dt} = \left. {\left( { - \frac{1}{{3000}}{t^4} + \frac{{19}}{{600}}{t^3} - \frac{{19}}{{120}}{t^2}} \right)_0^{60}} \right| = 1950m\).
Bài tập 10 trang 43 SGK Toán 12 tập 2 - Cánh diều thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp để giải quyết các bài toán cụ thể.
Bài tập 10 thường bao gồm các dạng bài sau:
Để giải quyết bài tập 10 trang 43 một cách hiệu quả, bạn cần nắm vững các kiến thức và kỹ năng sau:
Bài toán: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Lời giải:
f'(x) = 3x2 + 4x - 5
Ngoài các bài tập cơ bản, bạn cũng có thể gặp các bài tập nâng cao hơn, yêu cầu bạn vận dụng đạo hàm để giải quyết các bài toán phức tạp hơn, chẳng hạn như:
Để đạt được kết quả tốt nhất, bạn nên:
Ngoài SGK Toán 12 tập 2 - Cánh diều, bạn có thể tham khảo thêm các tài liệu sau:
Bài tập 10 trang 43 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng, giúp bạn củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng rằng với những hướng dẫn và ví dụ minh họa trên, bạn sẽ tự tin giải quyết bài tập này một cách hiệu quả.