Lý thuyết Giá trị lớn nhất - nhỏ nhất hàm số Toán 12 Cánh Diều

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cánh Diều

Chào mừng bạn đến với bài học về lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trong chương trình Toán 12 Cánh Diều. Đây là một chủ đề quan trọng, thường xuyên xuất hiện trong các kỳ thi THPT Quốc gia.

Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về cách xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số, các phương pháp giải bài toán liên quan và các ví dụ minh họa cụ thể.

1. Định nghĩa Khái niệm GTLN, GTNN của hàm số

1. Định nghĩa

Khái niệm GTLN, GTNN của hàm số

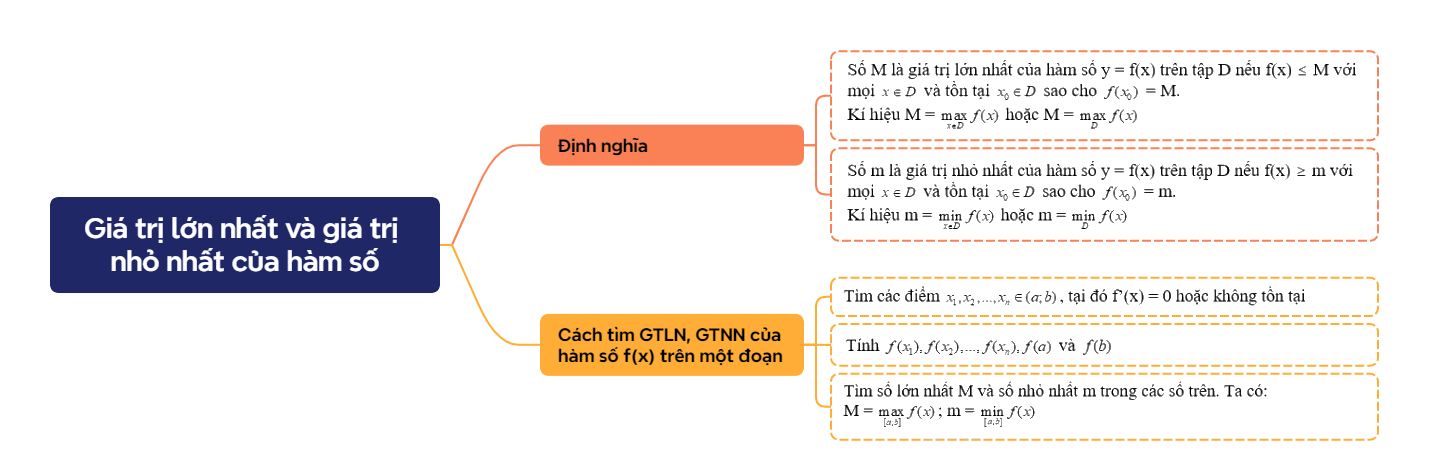
Cho hàm số y = f(x) xác định trên tập D.

- Số M là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) \( \le \) M với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f({x_0})\) = M.

Kí hiệu M = \(\mathop {\max }\limits_{x \in D} f(x)\) hoặc M = \(\mathop {\max }\limits_D f(x)\)

- Số m là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) \( \ge \) m với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f({x_0})\) = m.

Kí hiệu m = \(\mathop {\min }\limits_{x \in D} f(x)\) hoặc m = \(\mathop {\min }\limits_D f(x)\)

2. Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Để tìm GTLN, GTNN của hàm số f(x) trên một khoảng, đoạn hay nửa khoảng, ta có thể lập bảng biến thiên của hàm số trên tập hợp đó. Căn cứ vào bảng biến thiên, ta tìm được GTLN và GTNN (nếu có) của hàm số

Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn \(\left[ {a;b} \right]\):

Tìm các điểm \({x_1},{x_2},...,{x_n} \in (a;b)\), tại đó f’(x) = 0 hoặc không tồn tại
Tính \(f({x_1}),f({x_2}),...,f({x_n}),f(a)\) và \(f(b)\)
Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:

M = \(\mathop {\max }\limits_{\left[ {a;b} \right]} f(x)\); m = \(\mathop {\min }\limits_{\left[ {a;b} \right]} f(x)\)

Ví dụ: Tìm GTLN và GTNN của hàm số \(y = {x^4} - 4{x^2} + 3\) trên đoạn \(\left[ {0;4} \right]\)

Ta có: \(y' = 4{x^3} - 8x = 4x({x^2} - 2);y' = 0 \Leftrightarrow x = 0\) hoặc \(x = \sqrt 2 \) (vì \(x \in \left[ {0;4} \right]\))

y(0) = 3; y(4) = 195; y(\(\sqrt 2 \)) = -1

Do đó: \(\mathop {\max }\limits_{\left[ {0;4} \right]} y = y(4) = 195\); \(\mathop {\min }\limits_{\left[ {0;4} \right]} y = y(\sqrt 2 ) = - 1\)

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cánh Diều 1

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cánh Diều đặc sắc thuộc chuyên mục bài toán lớp 12 trên nền tảng toán math. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cánh Diều

Trong chương trình Toán 12, chủ đề Giá trị lớn nhất và giá trị nhỏ nhất của hàm số đóng vai trò quan trọng, giúp học sinh rèn luyện tư duy logic và kỹ năng giải quyết vấn đề. Bài viết này sẽ trình bày chi tiết lý thuyết, phương pháp giải và các bài tập minh họa thuộc chương trình Cánh Diều.

I. Khái niệm cơ bản

1. Giá trị lớn nhất (Maximum Value): Điểm x₀ được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng mở (a, b) chứa x₀ sao cho f(x) ≤ f(x₀) với mọi x thuộc (a, b). Giá trị f(x₀) được gọi là giá trị lớn nhất của hàm số trên khoảng (a, b).

2. Giá trị nhỏ nhất (Minimum Value): Điểm x₀ được gọi là điểm cực tiểu của hàm số f(x) nếu tồn tại một khoảng mở (a, b) chứa x₀ sao cho f(x) ≥ f(x₀) với mọi x thuộc (a, b). Giá trị f(x₀) được gọi là giá trị nhỏ nhất của hàm số trên khoảng (a, b).

3. Cực trị của hàm số: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số được gọi chung là cực trị của hàm số.

II. Điều kiện để hàm số đạt cực trị

Để hàm số f(x) đạt cực trị tại điểm x₀, cần có điều kiện sau:

x₀ là điểm dừng của hàm số, tức là f'(x₀) = 0.
Đạo hàm bậc hai tại x₀ khác 0, tức là f''(x₀) ≠ 0.

Nếu f''(x₀) > 0 thì x₀ là điểm cực tiểu.

Nếu f''(x₀) < 0 thì x₀ là điểm cực đại.

III. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn [a, b]

Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [a, b], ta thực hiện các bước sau:

Tính đạo hàm f'(x).
Tìm các điểm dừng của hàm số bằng cách giải phương trình f'(x) = 0.
Kiểm tra xem các điểm dừng có thuộc đoạn [a, b] hay không.
Tính giá trị của hàm số tại các điểm dừng thuộc đoạn [a, b] và tại hai đầu mút của đoạn [a, b], tức là f(a) và f(b).
So sánh các giá trị vừa tính được để tìm ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [a, b].

IV. Các dạng bài tập thường gặp

1. Tìm cực trị của hàm số: Bài tập yêu cầu tìm các điểm cực đại, cực tiểu và giá trị tương ứng của hàm số.

2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn: Bài tập yêu cầu tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn cho trước.

3. Bài toán ứng dụng: Bài tập liên quan đến các bài toán thực tế, yêu cầu sử dụng kiến thức về giá trị lớn nhất và giá trị nhỏ nhất để giải quyết.

V. Ví dụ minh họa

Ví dụ 1: Tìm cực trị của hàm số f(x) = x³ - 3x² + 2.

Giải:

f'(x) = 3x² - 6x
f'(x) = 0 ⇔ 3x² - 6x = 0 ⇔ x = 0 hoặc x = 2
f''(x) = 6x - 6
f''(0) = -6 < 0 ⇒ x = 0 là điểm cực đại, f(0) = 2
f''(2) = 6 > 0 ⇒ x = 2 là điểm cực tiểu, f(2) = -2

Vậy hàm số đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.

VI. Lưu ý khi giải bài tập

Luôn kiểm tra điều kiện xác định của hàm số.
Chú ý đến các trường hợp đặc biệt như hàm số không có đạo hàm tại một số điểm.
Sử dụng các phương pháp đại số và hình học để hỗ trợ giải quyết bài toán.

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cánh Diều. Chúc bạn học tập tốt!