Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 1 - Cánh diều. Bài viết này sẽ hướng dẫn bạn giải bài tập 9 trang 73 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết và dễ tiếp thu nhất.
Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao 30 m và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn.
Đề bài
Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao 30 m và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn.
Mô hình thiết kế được xây dựng như sau: Trong hệ trục toạ độ \(Oxyz\) (đơn vị độ dài trên mỗi trục là 1 m), các đỉnh của bốn chiếc cột lần lượt là các điểm \(M\left( {90;0;30} \right),N\left( {90;120;30} \right)\),\(P\left( {0;\;120;\;30} \right),Q\left( {0;\;0;\;30} \right)\) (Hình 34)
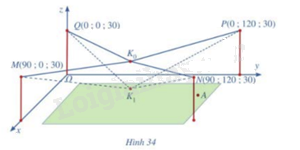
Giả sử \({K_0}\) là vị trí ban đầu của camera có cao độ bằng 25 và \({K_0}M = {K_0}N = {K_0}P = {K_0}Q\). Để theo dõi quả bóng đến vị trí \(A\), camera được hạ thấp theo phương thẳng đứng xuống điểm \({K_1}\) cao độ bằng 19. tìm các điểm \({K_0},{K_1}\) và vector \(\overrightarrow {{K_0}{K_1}} \)
Phương pháp giải - Xem chi tiết
Trong không gian với hệ toạ độ Oxyz, cho điểm M.
Xác định hình chiếu M, của điểm M trên mặt phẳng Oxy. Trong mặt phẳng toạ độ Oxy, tìm hoành độ a, tung độ b của điểm M₁.
Xác định hình chiếu P của điểm M trên trục cao Oz, điểm P ứng với số c trên trục Oz. Số c là cao độ của điểm M.
Bộ số (a; b; c) là toạ độ của điểm M trong không gian với hệ toạ độ Oxyz, kí hiệu là M(a; b; c).
Lời giải chi tiết
Đầu tiên, chúng ta cần xác định vị trí ban đầu của camera, điểm \({K_0}\). Vì\(\;{K_0}M = {K_0}N = {K_0}P = {K_0}Q\), nghĩa là \({K_0}\) nằm ở trung tâm của hình hộp chữ nhật tạo bởi \(M,N,P,Q\). Do đó, tọa độ của \({K_0}\) sẽ là trung bình cộng của tọa độ của \(M,N,P,Q\).
Tọa độ của \({K_0}\) sẽ là:
\({K_0} = \left( {\frac{{90 + 90 + 0 + 0}}{4},\frac{{0 + 120 + 120 + 0}}{4},25} \right) = \left( {45,60,25} \right)\)
Tiếp theo, chúng ta cần xác định vị trí của camera sau khi nó được hạ xuống, điểm \({K_1}\). Vì camera được hạ theo phương thẳng đứng, nên tọa độ x và y của \({K_1}\) sẽ giống như \({K_0}\), chỉ có tọa độ z (cao độ) thay đổi.
Vậy tọa độ của\(\;{K_1}\) sẽ là: \({K_1}\left( {45,60,19} \right)\)
Cuối cùng, vector từ \({K_0}\) đến \({K_1}\), \(\overrightarrow {{K_0}{K_1}} \), sẽ là:
\(\overrightarrow {{K_0}{K_1}} = \;{K_1} - {K_0} = \left( {0,0,19 - 25} \right) = \left( {0,0, - 6} \right)\)
Vậy, điểm ban đầu của camera là \({K_0}\left( {45,\;60,\;25} \right)\), điểm sau khi camera được hạ xuống là \({K_1}\left( {45,\;60,\;19} \right)\) và vector từ \({K_0}\) đến \({K_1}\) là \(\overrightarrow {{K_0}{K_1}} \left( {0,0, - 6} \right).\)
Bài tập 9 trang 73 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về giới hạn của hàm số. Đây là một chủ đề quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn. Để giải quyết bài tập này, học sinh cần nắm vững các khái niệm về giới hạn, giới hạn một bên, và các tính chất của giới hạn.
Bài tập yêu cầu tính giới hạn của hàm số tại một điểm cho trước. Cụ thể, bài tập có thể có dạng:
Trong đó, f(x) là một hàm số cụ thể và a là một giá trị thực.
Ví dụ: Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
Ta có:
limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2)
Vì x ≠ 2, ta có thể rút gọn biểu thức:
limx→2 (x + 2) = 2 + 2 = 4
Vậy, limx→2 (x2 - 4) / (x - 2) = 4
Ngoài SGK Toán 12 tập 1 - Cánh diều, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài tập 9 trang 73 SGK Toán 12 tập 1 - Cánh diều. Chúc bạn học tập tốt!