Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 28, 29, 30 sách giáo khoa Toán 12 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Tính diện tích hình phẳng
Trả lời câu hỏi Hoạt động 1 trang 28 SGK Toán 12 Cánh diều
Cho hàm số \(y = f(x) = {x^3} - 2{x^2} - x + 2\) có đồ thị minh họa ở Hình 11.

a) Quan sát Hình 11, hãy cho biết các hình phẳng \({H_1},{H_2},{H_3}\) lần lượt được giới hạn bởi các đường thẳng và đồ thị hàm số nào
b) Tính diện tích \({S_{{H_1}}},{S_{{H_2}}},{S_{{H_3}}}\) của các hình phẳng đó
c) Gọi H là tập hợp của các hình phẳng \({H_1},{H_2},{H_3}\). Hình phẳng H được gọi là hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và các đường thẳng x = 0, x = 3. Chứng tỏ rằng diện tích \({S_H}\) của hình phẳng H bằng \({S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^3 {\left| {f(x)} \right|dx} \)
Phương pháp giải:
a) Quan sát hình vẽ
b) Sử dụng công thức tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b là: \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)
c) Sử dụng tính chất của tích phân \(\int\limits_a^b {f(x)} dx = \int\limits_a^c {f(x)} dx + \int\limits_c^b {f(x)} dx\)
Lời giải chi tiết:
a) Hình \({H_1}\) được giới hạn bởi các đường thẳng x = 0, x = 1 và đồ thị hàm số y = f(x)
Hình \({H_2}\) được giới hạn bởi các đường thẳng x = 1, x = 2 và đồ thị hàm số y = f(x)
Hình \({H_3}\) được giới hạn bởi các đường thẳng x = 2, x = 3 và đồ thị hàm số y = f(x)
b) \({S_{{H_1}}} = \int\limits_0^1 {f(x)dx} = \int\limits_0^1 {\left( {{x^3} - 2{x^2} - x + 2} \right)dx} = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_0^1 = \frac{{13}}{{12}}\)
\(\int\limits_1^2 {f(x)dx = \int\limits_1^2 {\left( {{x^3} - 2{x^2} - x + 2} \right)} } dx = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_1^2 = - \frac{5}{{12}} \to {S_{{H_2} = }}\frac{5}{{12}}\)
\({S_{{H_3}}} = \int\limits_2^3 {f(x)dx = \int\limits_2^3 {\left( {{x^3} - 2{x^2} - x + 2} \right)} } dx = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_2^3 = \frac{{37}}{{12}}\)
c) \({S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^1 {f(x)dx} + \left| {\int\limits_1^2 {f(x)dx} } \right| + \int\limits_2^3 {f(x)dx} = \int\limits_0^3 {\left| {f(x)} \right|dx} \)
Trả lời câu hỏi Hoạt động 2 trang 30 SGK Toán 12 Cánh diều
Cho các hàm số \(y = {2^x}\), y = x
Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số \(y = {2^x}\)
Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số y = x
Gọi S là phẳng giới hạn bởi các đồ thị hàm số \(y = {2^x}\), y = x và hai đường thẳng x = 1, x = 2
(Hình 14)
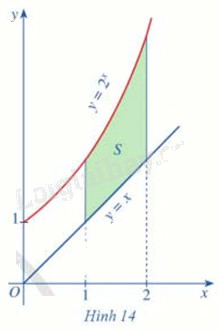
a) Biểu diễn S theo \({S_1},{S_2}\)
b) So sánh S và \(\int\limits_1^2 {({2^x} - x)dx} \)
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
a) \(S = {S_1} - {S_2}\)
b) \(S = {S_1} - {S_2}\)
\(\int\limits_1^2 {({2^x} - x)dx} = \int\limits_1^2 {{2^x}dx} - \int\limits_1^2 {xdx} = {S_1} - {S_2}\)
Vậy S = \(\int\limits_1^2 {({2^x} - x)dx} \)
Trả lời câu hỏi Hoạt động 1 trang 28 SGK Toán 12 Cánh diều
Cho hàm số \(y = f(x) = {x^3} - 2{x^2} - x + 2\) có đồ thị minh họa ở Hình 11.

a) Quan sát Hình 11, hãy cho biết các hình phẳng \({H_1},{H_2},{H_3}\) lần lượt được giới hạn bởi các đường thẳng và đồ thị hàm số nào
b) Tính diện tích \({S_{{H_1}}},{S_{{H_2}}},{S_{{H_3}}}\) của các hình phẳng đó
c) Gọi H là tập hợp của các hình phẳng \({H_1},{H_2},{H_3}\). Hình phẳng H được gọi là hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và các đường thẳng x = 0, x = 3. Chứng tỏ rằng diện tích \({S_H}\) của hình phẳng H bằng \({S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^3 {\left| {f(x)} \right|dx} \)
Phương pháp giải:
a) Quan sát hình vẽ
b) Sử dụng công thức tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b là: \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)
c) Sử dụng tính chất của tích phân \(\int\limits_a^b {f(x)} dx = \int\limits_a^c {f(x)} dx + \int\limits_c^b {f(x)} dx\)
Lời giải chi tiết:
a) Hình \({H_1}\) được giới hạn bởi các đường thẳng x = 0, x = 1 và đồ thị hàm số y = f(x)
Hình \({H_2}\) được giới hạn bởi các đường thẳng x = 1, x = 2 và đồ thị hàm số y = f(x)
Hình \({H_3}\) được giới hạn bởi các đường thẳng x = 2, x = 3 và đồ thị hàm số y = f(x)
b) \({S_{{H_1}}} = \int\limits_0^1 {f(x)dx} = \int\limits_0^1 {\left( {{x^3} - 2{x^2} - x + 2} \right)dx} = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_0^1 = \frac{{13}}{{12}}\)
\(\int\limits_1^2 {f(x)dx = \int\limits_1^2 {\left( {{x^3} - 2{x^2} - x + 2} \right)} } dx = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_1^2 = - \frac{5}{{12}} \to {S_{{H_2} = }}\frac{5}{{12}}\)
\({S_{{H_3}}} = \int\limits_2^3 {f(x)dx = \int\limits_2^3 {\left( {{x^3} - 2{x^2} - x + 2} \right)} } dx = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_2^3 = \frac{{37}}{{12}}\)
c) \({S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^1 {f(x)dx} + \left| {\int\limits_1^2 {f(x)dx} } \right| + \int\limits_2^3 {f(x)dx} = \int\limits_0^3 {\left| {f(x)} \right|dx} \)
Trả lời câu hỏi Hoạt động 2 trang 30 SGK Toán 12 Cánh diều
Cho các hàm số \(y = {2^x}\), y = x
Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số \(y = {2^x}\)
Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số y = x
Gọi S là phẳng giới hạn bởi các đồ thị hàm số \(y = {2^x}\), y = x và hai đường thẳng x = 1, x = 2
(Hình 14)
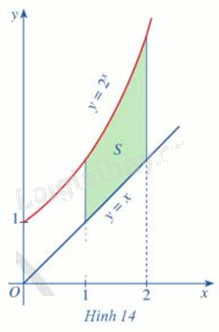
a) Biểu diễn S theo \({S_1},{S_2}\)
b) So sánh S và \(\int\limits_1^2 {({2^x} - x)dx} \)
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
a) \(S = {S_1} - {S_2}\)
b) \(S = {S_1} - {S_2}\)
\(\int\limits_1^2 {({2^x} - x)dx} = \int\limits_1^2 {{2^x}dx} - \int\limits_1^2 {xdx} = {S_1} - {S_2}\)
Vậy S = \(\int\limits_1^2 {({2^x} - x)dx} \)
Mục 1 của chương trình Toán 12 tập 2 - Cánh diều tập trung vào các kiến thức về số phức. Nội dung bao gồm định nghĩa số phức, các phép toán trên số phức (cộng, trừ, nhân, chia), và các ứng dụng của số phức trong giải phương trình đa thức. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học nâng cao hơn.
Trang 28 SGK Toán 12 tập 2 - Cánh diều bao gồm các bài tập về biểu diễn số phức trên mặt phẳng phức. Các bài tập này yêu cầu học sinh vận dụng kiến thức về phần thực, phần ảo của số phức và mối liên hệ giữa số phức và điểm trên mặt phẳng phức.
Trang 29 SGK Toán 12 tập 2 - Cánh diều tập trung vào các bài tập về phép cộng, trừ số phức. Học sinh cần nắm vững quy tắc cộng, trừ số phức bằng cách cộng, trừ các phần thực và phần ảo tương ứng.
Trang 30 SGK Toán 12 tập 2 - Cánh diều giới thiệu các bài tập về phép nhân, chia số phức. Đây là phần kiến thức khó hơn, đòi hỏi học sinh phải nắm vững các quy tắc nhân, chia số phức và sử dụng liên hợp của số phức để thực hiện phép chia.
| Bài tập | Lời giải |
|---|---|
| Bài 4: (1 + i)(2 - 3i) | (1 + i)(2 - 3i) = 1*2 + 1*(-3i) + i*2 + i*(-3i) = 2 - 3i + 2i - 3i2 = 2 - i - 3(-1) = 2 - i + 3 = 5 - i |
| Bài 5: (3 - 2i)/(1 + i) | (3 - 2i)/(1 + i) = (3 - 2i)(1 - i)/((1 + i)(1 - i)) = (3 - 3i - 2i + 2i2)/(1 - i2) = (3 - 5i - 2)/(1 + 1) = (1 - 5i)/2 = 0.5 - 2.5i |
Để giải tốt các bài tập về số phức, các em cần:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ tự tin hơn khi giải các bài tập về số phức trong SGK Toán 12 tập 2 - Cánh diều. Chúc các em học tập tốt!