Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 1 - Cánh diều. Bài tập 10 trang 47 thuộc chương trình học quan trọng, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải dễ hiểu, kèm theo các bước giải chi tiết, giúp bạn nắm bắt phương pháp giải bài tập một cách hiệu quả.
Một trang sách có dạng hình chữ nhật với diện tích là 384 cm². Sau khi để lề trên và lề dưới đều là 3 cm, để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Kích thước tối ưu của trang sách là bao nhiêu để phần in chữ trên trang sách có diện tích lớn nhất?
Đề bài
Một trang sách có dạng hình chữ nhật với diện tích là 384 cm². Sau khi để lề trên và lề dưới đều là 3 cm, để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Kích thước tối ưu của trang sách là bao nhiêu để phần in chữ trên trang sách có diện tích lớn nhất?
Phương pháp giải - Xem chi tiết
Phân tích đề bài.
Tìm các mối quan hệ trong bài.
Lập phương trình và giải.
Lời giải chi tiết
Giả sử chiều rộng của trang sách là x và chiều dài là y. Theo đề bài, diện tích của trang sách là:
$xy~=~384~cm{}^\text{2}$.
Khi để lề trên và lề dưới đều là 3 cm, lề trái và lề phải đều là 2 cm thì diện tích phần in chữ sẽ là:
\(\left( {y - 2.3} \right)\left( {x - 2.2} \right)\; = \;\left( {y - 6} \right)\left( {x - 4} \right)\)
Ta có: \(x = \frac{{384}}{y}\).
Thay x vào phương trình \(\left( {y - 6} \right)\left( {x - 4} \right)\) ta thu được \(\left( {x - 4} \right)\left( {\frac{{384}}{x} - 6} \right)\).
Xét \(f\left( x \right) = \;\left( {x - 4} \right)\left( {\frac{{384}}{x} - 6} \right)\)
\( = \frac{{ - 6{x^2} + 408x - 1536}}{x}\) với \(x \in (4;64)\) do \(\left\{ {\begin{array}{*{20}{c}}{x - 4 > 0}\\{\frac{{384}}{x} - 6 > 0}\end{array}} \right.\).
Ta có: \(f'(x) = \frac{{ - 6{x^2} + 1536}}{{{x^2}}} = 0 \Leftrightarrow x = \pm 16\). Với \(x \in (4;64)\) thì chỉ xét x = 16.
Ta có bảng biến thiên:
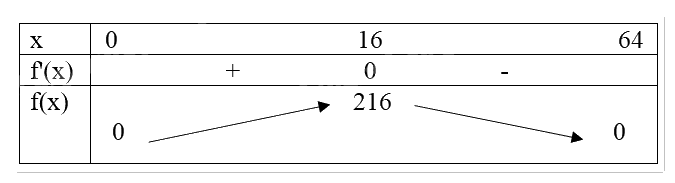
Với \(x = 16\) thì \(y = \frac{{384}}{x} = \frac{{384}}{{16}} = 24\).
Vậy kích thước của trang sách có chiều dài 24 cm, chiều rộng 16 cm thì phần in chữ trên trang sách có diện tích lớn nhất.
Bài tập 10 trang 47 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về Đạo hàm của hàm số. Đây là một trong những chủ đề quan trọng, nền tảng cho việc học tập các kiến thức toán học nâng cao hơn. Bài tập này thường yêu cầu học sinh vận dụng các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp.
Bài tập 10 thường bao gồm các dạng bài sau:
Để giải quyết bài tập 10 trang 47 SGK Toán 12 tập 1 - Cánh diều một cách hiệu quả, bạn cần nắm vững các kiến thức và kỹ năng sau:
Bài tập: Tính đạo hàm của hàm số f(x) = x^3 + 2x^2 - 5x + 1.
Giải:
f'(x) = (x^3)' + (2x^2)' - (5x)' + (1)'
f'(x) = 3x^2 + 4x - 5 + 0
f'(x) = 3x^2 + 4x - 5
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài tập 10 trang 47 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng, giúp bạn rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng với những hướng dẫn và ví dụ minh họa trên, bạn sẽ tự tin hơn khi giải quyết bài tập này. Chúc bạn học tập tốt!