Chào mừng các em học sinh đến với lời giải chi tiết bài tập 3 trang 92 SGK Toán 12 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 12.
Bài tập 3 thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm.
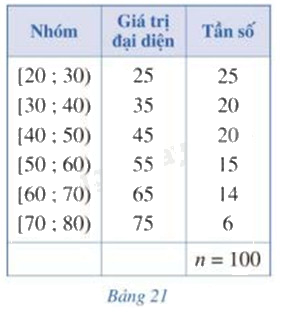
Bảng 21 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố. Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
Đề bài
Bảng 21 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố. Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
Phương pháp giải - Xem chi tiết
\({s^2} = \frac{{{n_1}.{{({x_1} - \overline x )}^2} + {n_2}{{({x_2} - \overline x )}^2} + ... + {n_p}{{({x_p} - \overline x )}^2}}}{n}\)
\(s = \sqrt {{s^2}} \)
Lời giải chi tiết
Số trung bình cộng của mẫu số liệu ghép nhóm là: \(\overline x = \frac{{25.25 + 20.35 + 20.45 + 15.55 + 14.65 + 6.75}}{{100}} = 44,1\)
Phương sai của mẫu số liệu ghép nhóm là:
\({s^2} = \frac{{25.{{(25 - 44,1)}^2} + 20.{{(35 - 44,1)}^2} + 20.{{(45 - 44,1)}^2} + 15.{{(55 - 44,1)}^2} + 14.{{(65 - 44,1)}^2} + 6.{{(75 - 44,1)}^2}}}{{100}} = 244,19\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(s = \sqrt {{s^2}} = \sqrt {244,19} \approx 15,63\)
Bài tập 3 trang 92 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số để giải quyết các bài toán cụ thể. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Bài tập 3 bao gồm các câu hỏi yêu cầu học sinh tính đạo hàm của các hàm số sau:
Để giải bài tập này, học sinh có thể áp dụng các phương pháp sau:
Câu a: y = x4 + 5x2 - 3
y' = 4x3 + 10x
Câu b: y = (2x - 1)(x2 + 3)
y' = 2(x2 + 3) + (2x - 1)(2x) = 2x2 + 6 + 4x2 - 2x = 6x2 - 2x + 6
Câu c: y = (x2 + 1) / (x - 2)
y' = [(2x)(x - 2) - (x2 + 1)(1)] / (x - 2)2 = (2x2 - 4x - x2 - 1) / (x - 2)2 = (x2 - 4x - 1) / (x - 2)2
Câu d: y = sin(2x) + cos(x)
y' = 2cos(2x) - sin(x)
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài tập 3 trang 92 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.