Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 81, 82 sách giáo khoa Toán 12 tập 2 chương trình Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Hình 38 mô tả một mặt cầu trong không gian. Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu được lập như thế nào?
Trả lời câu hỏi Luyện tập 1 trang 82 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 3) và mặt cầu tâm I đi qua điểm A(0; 4; 5). Tính bán kính R của mặt cầu đó.
Phương pháp giải:
Sử dụng kiến thức về vị trí của điểm so với mặt cầu để tìm bán kính của mặt cầu: Cho mặt cầu tâm I, bán kính R và điểm M bất kì trong không gian. Điểm M thuộc mặt cầu tâm I, bán kính R khi và chỉ khi \(IM = R\).
Lời giải chi tiết:
Vì mặt cầu tâm I đi qua điểm A nên IA là bán kính của mặt cầu.
Bán kính của mặt cầu là: \(R = IA = \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( {4 - 2} \right)}^2} + {{\left( {5 - 3} \right)}^2}} = 3\).
Trả lời câu hỏi khởi động trang 81 SGK Toán 12 Cánh diều
Hình 38 mô tả một mặt cầu trong không gian.
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu được lập như thế nào?

Phương pháp giải:
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu tâm I(a; b; c) bán kính R là: \(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R\).
Lời giải chi tiết:
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu tâm I(a; b; c) bán kính R là: \(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R\).
Trả lời câu hỏi Hoạt động 1 trang 81 SGK Toán 12 Cánh diều
Nếu quay đường tròn tâm I bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?
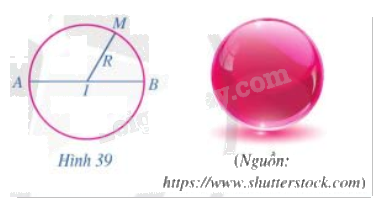
Phương pháp giải:
Khi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
Lời giải chi tiết:
Khi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
Trả lời câu hỏi khởi động trang 81 SGK Toán 12 Cánh diều
Hình 38 mô tả một mặt cầu trong không gian.
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu được lập như thế nào?

Phương pháp giải:
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu tâm I(a; b; c) bán kính R là: \(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R\).
Lời giải chi tiết:
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu tâm I(a; b; c) bán kính R là: \(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R\).
Trả lời câu hỏi Hoạt động 1 trang 81 SGK Toán 12 Cánh diều
Nếu quay đường tròn tâm I bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?
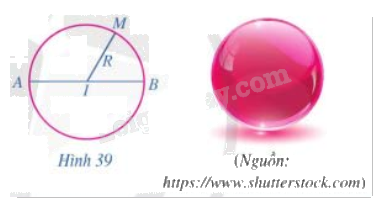
Phương pháp giải:
Khi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
Lời giải chi tiết:
Khi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
Trả lời câu hỏi Luyện tập 1 trang 82 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 3) và mặt cầu tâm I đi qua điểm A(0; 4; 5). Tính bán kính R của mặt cầu đó.
Phương pháp giải:
Sử dụng kiến thức về vị trí của điểm so với mặt cầu để tìm bán kính của mặt cầu: Cho mặt cầu tâm I, bán kính R và điểm M bất kì trong không gian. Điểm M thuộc mặt cầu tâm I, bán kính R khi và chỉ khi \(IM = R\).
Lời giải chi tiết:
Vì mặt cầu tâm I đi qua điểm A nên IA là bán kính của mặt cầu.
Bán kính của mặt cầu là: \(R = IA = \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( {4 - 2} \right)}^2} + {{\left( {5 - 3} \right)}^2}} = 3\).
Mục 1 trang 81, 82 SGK Toán 12 tập 2 - Cánh diều tập trung vào việc ôn tập chương trình Giải tích, bao gồm các kiến thức về đạo hàm, tích phân và ứng dụng của chúng. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các công thức, định lý đã học để giải quyết các bài toán thực tế.
Bài tập này yêu cầu học sinh tính đạo hàm của các hàm số, tìm cực trị của hàm số và khảo sát hàm số. Để giải quyết bài tập này, học sinh cần nắm vững các quy tắc tính đạo hàm, các điều kiện để hàm số có cực trị và các bước khảo sát hàm số.
Bài tập này yêu cầu học sinh tính tích phân xác định, tích phân bất định và ứng dụng tích phân để tính diện tích hình phẳng. Để giải quyết bài tập này, học sinh cần nắm vững các công thức tính tích phân, các phương pháp tính tích phân và các ứng dụng của tích phân.
Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm và tích phân để giải quyết các bài toán thực tế, chẳng hạn như bài toán tối ưu hóa, bài toán tính diện tích, thể tích. Để giải quyết bài tập này, học sinh cần phân tích bài toán, xây dựng mô hình toán học và sử dụng các công cụ đạo hàm, tích phân để giải quyết bài toán.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 81, 82 SGK Toán 12 tập 2 - Cánh diều:
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Lời giải chi tiết bài 1) |
| Bài 2 | (Lời giải chi tiết bài 2) |
| Bài 3 | (Lời giải chi tiết bài 3) |
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 1 trang 81, 82 SGK Toán 12 tập 2 - Cánh diều. Chúc các em học tập tốt!