Giải bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều

Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều. Bài tập này thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về giới hạn của hàm số.

Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho hình hộp ABCD. A’B’C’D’. Vecto (vec u = overrightarrow {AA'} + overrightarrow {A'B'} + overrightarrow {A'D'} ) bằng vecto nào dưới đây? (a,overrightarrow {A'C;}) b.(overrightarrow {CA'} ) c.(overrightarrow {AC'} ) d,(overrightarrow {C'A} )

Đề bài

Cho hình hộp ABCD. A’B’C’D’. Vecto \(\vec u = \overrightarrow {AA'} + \overrightarrow {A'B'} + \overrightarrow {A'D'} \) bằng vecto nào dưới đây?

A. \(\overrightarrow {A'C}\)

B. \(\overrightarrow {CA'} \)

C. \(\overrightarrow {AC'} \)

D. \(\overrightarrow {C'A} \)

Phương pháp giải - Xem chi tiết Giải bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều 1

Vẽ hình.

Áp dụng quy tắc hình hộp.

Lời giải chi tiết

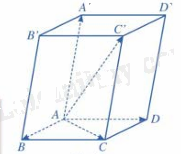
Giải bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều 2

Ta có:

\(\overrightarrow {AA'} + \overrightarrow {A'B'} + \overrightarrow {A'D'} \)

\(= \overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AD} \) (do \(\overrightarrow {A'B'} = \overrightarrow {AB}\), \(\overrightarrow {A'D'} = \overrightarrow {A'D'}\))

\(= \overrightarrow {A'C} \) (quy tắc hình hộp).

Chọn A

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều đặc sắc thuộc chuyên mục bài tập toán 12 trên nền tảng soạn toán. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều: Tổng quan

Bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để tính toán các giới hạn cụ thể. Đây là một bài tập quan trọng giúp củng cố lý thuyết và rèn luyện kỹ năng giải toán. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất và các phương pháp tính giới hạn đã học.

Nội dung bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều

Bài tập 1 bao gồm một số câu hỏi nhỏ, yêu cầu tính giới hạn của các hàm số khác nhau. Các hàm số này có thể là hàm đa thức, hàm hữu tỉ, hoặc các hàm số phức tạp hơn. Để giải quyết các bài toán này, học sinh có thể sử dụng các phương pháp sau:

Phương pháp trực tiếp: Thay trực tiếp giá trị của x vào hàm số để tính giới hạn.
Phương pháp phân tích thành nhân tử: Phân tích tử số và mẫu số thành nhân tử để rút gọn biểu thức và tính giới hạn.
Phương pháp nhân liên hợp: Nhân tử số và mẫu số với biểu thức liên hợp để khử dạng vô định.
Phương pháp sử dụng định lý giới hạn: Áp dụng các định lý giới hạn đã học để tính giới hạn.

Lời giải chi tiết bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều

Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều:

Câu a)

Tính lim_x→2 (x² - 4) / (x - 2)

Lời giải:

Phân tích tử số thành nhân tử: (x² - 4) = (x - 2)(x + 2)
Rút gọn biểu thức: (x² - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2
Tính giới hạn: lim_x→2 (x + 2) = 2 + 2 = 4

Câu b)

Tính lim_x→-1 (x³ + 1) / (x + 1)

Lời giải:

Phân tích tử số thành nhân tử: (x³ + 1) = (x + 1)(x² - x + 1)
Rút gọn biểu thức: (x³ + 1) / (x + 1) = (x + 1)(x² - x + 1) / (x + 1) = x² - x + 1
Tính giới hạn: lim_x→-1 (x² - x + 1) = (-1)² - (-1) + 1 = 1 + 1 + 1 = 3

Câu c)

Tính lim_x→0 sin(x) / x

Lời giải:

Đây là một giới hạn lượng giác cơ bản. Sử dụng định lý giới hạn đặc biệt, ta có: lim_x→0 sin(x) / x = 1

Lưu ý khi giải bài tập về giới hạn

Luôn kiểm tra xem biểu thức có dạng vô định hay không trước khi tính giới hạn.
Sử dụng các phương pháp phù hợp để đơn giản hóa biểu thức và tính giới hạn.
Nắm vững các định lý giới hạn và áp dụng chúng một cách chính xác.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Kết luận

Bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Bằng cách nắm vững các kiến thức lý thuyết và rèn luyện kỹ năng giải toán, các em có thể tự tin giải quyết các bài toán tương tự.

Hy vọng bài viết này đã cung cấp cho các em những thông tin hữu ích và giúp các em giải bài tập 1 trang 63 SGK Toán 12 tập 1 - Cánh diều một cách hiệu quả. Chúc các em học tập tốt!