Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1, trang 21, 22, 23 sách giáo khoa Toán 12 tập 1 - Cánh diều.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, khoa học, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Đường tiệm cận ngang
Trả lời câu hỏi Luyện tập 1 trang 22 SGK Toán 12 Cánh diều
Tìm tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x - 2}}{{x + 1}}\).
Phương pháp giải:
Đường thẳng \(y = {y_o}\) được gọi là đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_o}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_o}\).
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x + 1}} = 3\\\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{x + 1}} = 3\end{array} \right.\).
Vậy đường thẳng \(y = 3\) là tiệm cận ngang của đồ thị hàm số đã cho
Trả lời câu hỏi Hoạt động 1 trang 21 SGK Toán 12 Cánh diều
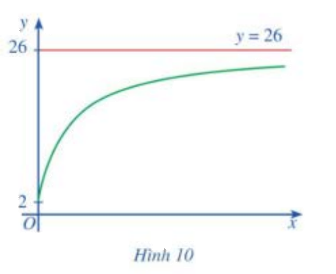
Xét hàm số \(y = f\left( x \right) = \frac{{26x + 10}}{{x + 5}}\) với \(x \in [0; + \infty )\) có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 26\)
Trả lời câu hỏi Hoạt động 1 trang 21 SGK Toán 12 Cánh diều
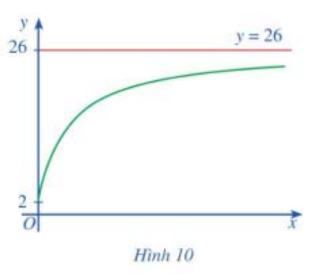
Xét hàm số \(y = f\left( x \right) = \frac{{26x + 10}}{{x + 5}}\) với \(x \in [0; + \infty )\) có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 26\)
Trả lời câu hỏi Luyện tập 1 trang 22 SGK Toán 12 Cánh diều
Tìm tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x - 2}}{{x + 1}}\).
Phương pháp giải:
Đường thẳng \(y = {y_o}\) được gọi là đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_o}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_o}\).
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x + 1}} = 3\\\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{x + 1}} = 3\end{array} \right.\).
Vậy đường thẳng \(y = 3\) là tiệm cận ngang của đồ thị hàm số đã cho
Mục 1 của SGK Toán 12 tập 1 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số và đồ thị. Đây là nền tảng quan trọng cho các kiến thức nâng cao hơn trong chương trình học. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là vô cùng cần thiết để đạt kết quả tốt trong các kỳ thi.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1, trang 21, 22, 23 SGK Toán 12 tập 1 - Cánh diều:
Đề bài: ... (Nội dung bài tập)
Lời giải: ... (Lời giải chi tiết, bao gồm các bước giải, giải thích rõ ràng)
Đề bài: ... (Nội dung bài tập)
Lời giải: ... (Lời giải chi tiết, bao gồm các bước giải, giải thích rõ ràng)
Đề bài: ... (Nội dung bài tập)
Lời giải: ... (Lời giải chi tiết, bao gồm các bước giải, giải thích rõ ràng)
Để giải tốt các bài tập trong Mục 1, các em cần nắm vững các phương pháp sau:
Ví dụ: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh của parabol.
Lời giải:
Hàm số y = x2 - 4x + 3 có dạng y = ax2 + bx + c với a = 1, b = -4, c = 3.
Tọa độ đỉnh của parabol là:
xđỉnh = -b / 2a = -(-4) / (2 * 1) = 2
yđỉnh = (2)2 - 4 * 2 + 3 = -1
Vậy tọa độ đỉnh của parabol là (2; -1).
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập và các đề thi thử.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em sẽ tự tin hơn trong việc học tập môn Toán 12. Chúc các em học tốt!