Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3, trang 54, 55 và 56 sách giáo khoa Toán 12 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Lập phương trình tổng quát của mặt phẳng biết một số điều kiện
Trả lời câu hỏi Hoạt động 7 trang 55 SGK Toán 12 Cánh diều
Cho ba điểm H(-1;1;2), I(1;3;2), K(-1;4;5) cùng thuộc mặt phẳng (P) (Hình 11)
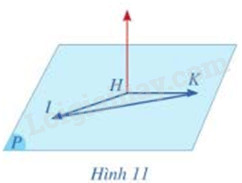
a) Tím tọa độ của các vecto \(\overrightarrow {HI} ,\overrightarrow {HK} \). Từ đó hãy chứng tỏ rằng ba điểm H, I, K không thẳng hàng
b) Lập phương trình mặt phẳng (P) đi qua điểm H(-1;1;2), biết cặp vecto chỉ phương là \(\overrightarrow {HI} ,\overrightarrow {HK} \)
Phương pháp giải:
a) \(A({a_1};{a_2};{a_3}),B({b_1};{b_2};{b_3}) \Rightarrow \overrightarrow {AB} = ({b_1} - {a_1};{b_2} - {a_2};{b_3} - {a_3})\)
b) Tìm vecto pháp tuyến của mặt phẳng \(\overrightarrow n = (A;B;C)\). Mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) và nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến có phương trình là \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
Lời giải chi tiết:
a) \(\overrightarrow {HI} = (2;2;0),\overrightarrow {HK} = (0;3;3)\)
Có \(\overrightarrow {HI} \ne k.\overrightarrow {HK} \) suy ra H, I, K không thẳng hàng
b) Vecto pháp tuyến của mặt phẳng (P) là: \(\overrightarrow n = [\overrightarrow {HI} ;\overrightarrow {HK} ] = (6; - 6;6)\)
Phương trình mặt phẳng (P) là: \(6(x + 1) - 6(y - 1) + 6(z - 2) = 0 \Leftrightarrow 6x - 6y + 6z = 0 \Leftrightarrow x - y + z = 0\)
Trả lời câu hỏi Hoạt động 6 trang 55 SGK Toán 12 Cánh diều
Cho mặt phẳng (P) đi qua điểm I(1;3;-2) có cặp vecto chỉ phương là \(\overrightarrow u = (1;1;3),\overrightarrow v = (2; - 1;2)\) (Hình 10)
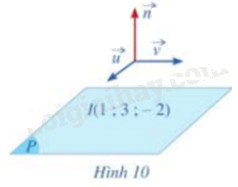
a) Hãy chỉ ra một vecto pháp tuyến \(\overrightarrow n \) của mặt phẳng (P)
b) Lập phương trình mặt phẳng (P) đi qua điểm I(1;3;-2) biết vecto pháp tuyển \(\overrightarrow n \)
Phương pháp giải:
a) Nếu hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) là cặp vecto chỉ phương của mặt phẳng (P) thì \(\overrightarrow n = [\overrightarrow u ;\overrightarrow v ] = \left( {\left| \begin{array}{l}{y_1}\;\;\;\;{z_1}\;\\{y_2}\;\;\;\;{z_2}\end{array} \right|;\left| \begin{array}{l}{z_1}\;\;\;\;{x_1}\\{x_2}\;\;\;\;{z_1}\end{array} \right|;\left| \begin{array}{l}{x_1}\;\;\;\;{y_1}\\{x_2}\;\;\;\;{y_2}\end{array} \right|} \right)\) là một vecto pháp tuyến của mặt phẳng (P)
b) Mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) và nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến có phương trình là \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
Lời giải chi tiết:
a) Vecto pháp tuyến của mặt phẳng (P) là \(\overrightarrow n = [\overrightarrow u ;\overrightarrow v ] = (5; - 4;3)\)
b) Phương trình mặt phẳng (P): \(5(x - 1) - 4(y - 3) + 3(z + 2) = 0 \Leftrightarrow 5x - 4y + 3z + 13 = 0\)
Trả lời câu hỏi Hoạt động 5 trang 54 SGK Toán 12 Cánh diều
Cho mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) có \(\overrightarrow n (A;B;C)\) là vecto pháp tuyến. Giả sử M(x;y;z) là một điểm bất kì thuộc mặt phẳng (P) (Hình 9)
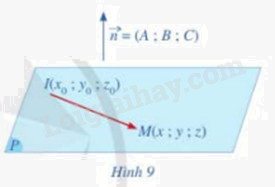
a) Tính tích vô hướng \(\overrightarrow n .\overrightarrow {IM} \)
b) Hãy biểu diễn \(\overrightarrow n .\overrightarrow {IM} \) theo \({x_0},{y_0},{z_0};x,y,z\) và A, B, C
Phương pháp giải:
Sử dụng công thức biểu thức tọa độ của tích vô hướng
Lời giải chi tiết:
a) \(\overrightarrow {IM} = (x - {x_0};y - {y_0};z - {z_0})\)
\(\overrightarrow n .\overrightarrow {IM} = A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0})\)
b) \(\overrightarrow n .\overrightarrow {IM} = A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = Ax + By + Cz - A{x_0} - B{y_0} - C{z_0}\)
Trả lời câu hỏi Hoạt động 5 trang 54 SGK Toán 12 Cánh diều
Cho mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) có \(\overrightarrow n (A;B;C)\) là vecto pháp tuyến. Giả sử M(x;y;z) là một điểm bất kì thuộc mặt phẳng (P) (Hình 9)
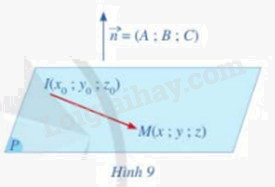
a) Tính tích vô hướng \(\overrightarrow n .\overrightarrow {IM} \)
b) Hãy biểu diễn \(\overrightarrow n .\overrightarrow {IM} \) theo \({x_0},{y_0},{z_0};x,y,z\) và A, B, C
Phương pháp giải:
Sử dụng công thức biểu thức tọa độ của tích vô hướng
Lời giải chi tiết:
a) \(\overrightarrow {IM} = (x - {x_0};y - {y_0};z - {z_0})\)
\(\overrightarrow n .\overrightarrow {IM} = A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0})\)
b) \(\overrightarrow n .\overrightarrow {IM} = A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = Ax + By + Cz - A{x_0} - B{y_0} - C{z_0}\)
Trả lời câu hỏi Hoạt động 6 trang 55 SGK Toán 12 Cánh diều
Cho mặt phẳng (P) đi qua điểm I(1;3;-2) có cặp vecto chỉ phương là \(\overrightarrow u = (1;1;3),\overrightarrow v = (2; - 1;2)\) (Hình 10)
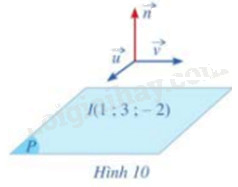
a) Hãy chỉ ra một vecto pháp tuyến \(\overrightarrow n \) của mặt phẳng (P)
b) Lập phương trình mặt phẳng (P) đi qua điểm I(1;3;-2) biết vecto pháp tuyển \(\overrightarrow n \)
Phương pháp giải:
a) Nếu hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) là cặp vecto chỉ phương của mặt phẳng (P) thì \(\overrightarrow n = [\overrightarrow u ;\overrightarrow v ] = \left( {\left| \begin{array}{l}{y_1}\;\;\;\;{z_1}\;\\{y_2}\;\;\;\;{z_2}\end{array} \right|;\left| \begin{array}{l}{z_1}\;\;\;\;{x_1}\\{x_2}\;\;\;\;{z_1}\end{array} \right|;\left| \begin{array}{l}{x_1}\;\;\;\;{y_1}\\{x_2}\;\;\;\;{y_2}\end{array} \right|} \right)\) là một vecto pháp tuyến của mặt phẳng (P)
b) Mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) và nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến có phương trình là \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
Lời giải chi tiết:
a) Vecto pháp tuyến của mặt phẳng (P) là \(\overrightarrow n = [\overrightarrow u ;\overrightarrow v ] = (5; - 4;3)\)
b) Phương trình mặt phẳng (P): \(5(x - 1) - 4(y - 3) + 3(z + 2) = 0 \Leftrightarrow 5x - 4y + 3z + 13 = 0\)
Trả lời câu hỏi Hoạt động 7 trang 55 SGK Toán 12 Cánh diều
Cho ba điểm H(-1;1;2), I(1;3;2), K(-1;4;5) cùng thuộc mặt phẳng (P) (Hình 11)
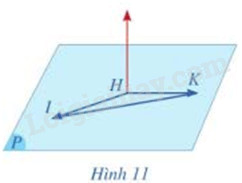
a) Tím tọa độ của các vecto \(\overrightarrow {HI} ,\overrightarrow {HK} \). Từ đó hãy chứng tỏ rằng ba điểm H, I, K không thẳng hàng
b) Lập phương trình mặt phẳng (P) đi qua điểm H(-1;1;2), biết cặp vecto chỉ phương là \(\overrightarrow {HI} ,\overrightarrow {HK} \)
Phương pháp giải:
a) \(A({a_1};{a_2};{a_3}),B({b_1};{b_2};{b_3}) \Rightarrow \overrightarrow {AB} = ({b_1} - {a_1};{b_2} - {a_2};{b_3} - {a_3})\)
b) Tìm vecto pháp tuyến của mặt phẳng \(\overrightarrow n = (A;B;C)\). Mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) và nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến có phương trình là \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
Lời giải chi tiết:
a) \(\overrightarrow {HI} = (2;2;0),\overrightarrow {HK} = (0;3;3)\)
Có \(\overrightarrow {HI} \ne k.\overrightarrow {HK} \) suy ra H, I, K không thẳng hàng
b) Vecto pháp tuyến của mặt phẳng (P) là: \(\overrightarrow n = [\overrightarrow {HI} ;\overrightarrow {HK} ] = (6; - 6;6)\)
Phương trình mặt phẳng (P) là: \(6(x + 1) - 6(y - 1) + 6(z - 2) = 0 \Leftrightarrow 6x - 6y + 6z = 0 \Leftrightarrow x - y + z = 0\)
Mục 3 trong SGK Toán 12 tập 2 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết và phân tích cách tiếp cận phù hợp.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập liên quan đến đạo hàm). Để giải bài này, ta thực hiện các bước sau:
Bài tập này liên quan đến... (giả sử bài tập liên quan đến tích phân). Lời giải:
Ta sử dụng phương pháp đổi biến số để tính tích phân này. Đặt t = ... Khi đó dt = ... Thay vào tích phân ban đầu, ta được...
Bài tập này yêu cầu học sinh tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Để giải quyết bài toán này, ta sử dụng phương pháp khảo sát hàm số:
Bài tập này là một bài toán ứng dụng thực tế liên quan đến... (giả sử bài tập liên quan đến tối ưu hóa). Để giải bài toán này, ta cần:
Bài tập này đòi hỏi học sinh phải kết hợp nhiều kiến thức khác nhau để giải quyết. Ví dụ, ta có thể cần sử dụng kiến thức về giới hạn, đạo hàm và tích phân.
Khi giải các bài tập trong mục 3, trang 54, 55, 56 SGK Toán 12 tập 2 - Cánh diều, các em cần lưu ý những điều sau:
Ngoài SGK Toán 12 tập 2 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 3, trang 54, 55, 56 SGK Toán 12 tập 2 - Cánh diều. Chúc các em học tập tốt!