Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 34, 35, 36 sách giáo khoa Toán 12 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Tính thể tích của hình khối
Trả lời câu hỏi Hoạt động 3 trang 34 SGK Toán 12 Cánh diều
Cắt khối lập phương có cạnh bằng 1 bởi một mặt phẳng tùy ý vuông góc với trục Ox tại x, với ta nhận được hình phẳng có diện tích là S(x) (Hình 17)
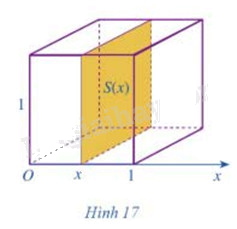
a) Tính S(x)
b) So sánh thể tích khối lập phương đó với \(\int\limits_0^1 {S(x)dx} \)
Phương pháp giải:
Sử dụng công thức tính diện tích hình vuông, thể tích hình lập phương và tích phân
Lời giải chi tiết:
a) S(x) = 1
b) Thể tích khối lập phương V = 1
\(\int\limits_0^1 {S(x)dx} = \int\limits_0^1 {1dx} = 1\)
Vậy thể tích khối lập phương đó = \(\int\limits_0^1 {S(x)dx} \)
Trả lời câu hỏi Hoạt động 3 trang 34 SGK Toán 12 Cánh diều
Cắt khối lập phương có cạnh bằng 1 bởi một mặt phẳng tùy ý vuông góc với trục Ox tại x, với ta nhận được hình phẳng có diện tích là S(x) (Hình 17)
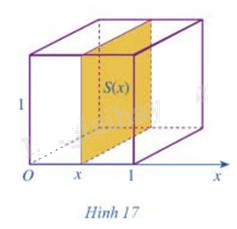
a) Tính S(x)
b) So sánh thể tích khối lập phương đó với \(\int\limits_0^1 {S(x)dx} \)
Phương pháp giải:
Sử dụng công thức tính diện tích hình vuông, thể tích hình lập phương và tích phân
Lời giải chi tiết:
a) S(x) = 1
b) Thể tích khối lập phương V = 1
\(\int\limits_0^1 {S(x)dx} = \int\limits_0^1 {1dx} = 1\)
Vậy thể tích khối lập phương đó = \(\int\limits_0^1 {S(x)dx} \)
Trả lời câu hỏi Hoạt động 4 trang 37 SGK Toán 12 Cánh diều
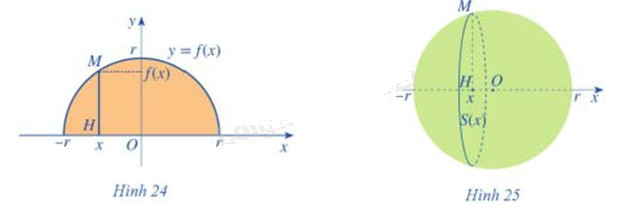
Xét hình tròn tâm O, bán kính r (Hình 24). Nửa hình tròn đó là hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y = f(x)
a) Tìm hàm số y = f(x)
b) Quay nửa hình tròn đó quanh trục hoành, ta nhận được hình cầu tâm O bán kính r (Hình 25). Xét điểm M(x;f(x)) \(( - r \le x \le r)\) nằm trên nửa đường tròn tâm O bán kính r. Gọi H(x;0) là hình chiếu của điểm M trên trục Ox. Khi quay nửa hình tròn quanh trục hoành, đoạn thẳng HM tạo nên một hình tròn tâm H bán kính f(x)
Tính diện tích S(x) của hình tròn đó theo f(x)
Từ đó, sử dụng công thức tính thể tích vật thể, hãy tính thể tích V của hình cầu tâm O bán kính r
Phương pháp giải:
a) Tìm hàm số y = f(x) thông qua phương trình nửa đường tròn
b) Sử dụng công thức tính thể tích hình cầu
Lời giải chi tiết:
a) Hàm số y = f(x) chính là phương trình của nửa đường tròn có tâm O, bán kính r
\( \Rightarrow y = f(x) = \sqrt {{r^2} - {x^2}} \)
b) \(S(x) = \pi {f^2}(x)\)
\(V = \frac{{4\pi {r^3}}}{3}\)
Trả lời câu hỏi Hoạt động 4 trang 37 SGK Toán 12 Cánh diều
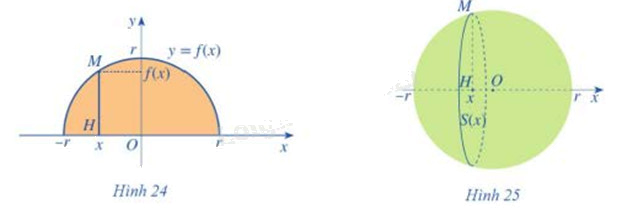
Xét hình tròn tâm O, bán kính r (Hình 24). Nửa hình tròn đó là hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y = f(x)
a) Tìm hàm số y = f(x)
b) Quay nửa hình tròn đó quanh trục hoành, ta nhận được hình cầu tâm O bán kính r (Hình 25). Xét điểm M(x;f(x)) \(( - r \le x \le r)\) nằm trên nửa đường tròn tâm O bán kính r. Gọi H(x;0) là hình chiếu của điểm M trên trục Ox. Khi quay nửa hình tròn quanh trục hoành, đoạn thẳng HM tạo nên một hình tròn tâm H bán kính f(x)
Tính diện tích S(x) của hình tròn đó theo f(x)
Từ đó, sử dụng công thức tính thể tích vật thể, hãy tính thể tích V của hình cầu tâm O bán kính r
Phương pháp giải:
a) Tìm hàm số y = f(x) thông qua phương trình nửa đường tròn
b) Sử dụng công thức tính thể tích hình cầu
Lời giải chi tiết:
a) Hàm số y = f(x) chính là phương trình của nửa đường tròn có tâm O, bán kính r
\( \Rightarrow y = f(x) = \sqrt {{r^2} - {x^2}} \)
b) \(S(x) = \pi {f^2}(x)\)
\(V = \frac{{4\pi {r^3}}}{3}\)
Mục 2 trong SGK Toán 12 tập 2 - Cánh diều thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết và phân tích các bước thực hiện.
(Giả sử đây là một bài tập về đạo hàm)
Để giải bài tập này, ta cần áp dụng quy tắc tính đạo hàm của hàm số. Cụ thể, ta sẽ sử dụng quy tắc đạo hàm của tổng, hiệu, tích, thương và quy tắc đạo hàm của hàm hợp. Sau khi tính được đạo hàm, ta sẽ thay giá trị của x vào để tìm ra kết quả cuối cùng.
(Giả sử đây là một bài tập về ứng dụng đạo hàm để khảo sát hàm số)
Để giải bài tập này, ta cần thực hiện các bước sau:
(Giả sử đây là một bài tập về tối ưu hóa)
Để giải bài tập tối ưu hóa, ta cần:
(Giả sử đây là một bài tập về tích phân)
Để giải bài tập tích phân, ta cần:
Khi giải bài tập Toán 12, các em cần lưu ý những điều sau:
Ngoài SGK Toán 12 tập 2 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!