Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2 trang 13 SGK Toán 12 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 12.
Bài tập 2 trang 13 thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về giới hạn của hàm số.
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau: Giá trị cực tiểu của hàm số đã cho bằng: a) \(2\). b) \(3\). c) \( - 4\). d) \(0\).
Đề bài
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau:
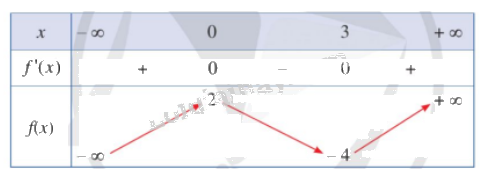 Giá trị cực tiểu của hàm số đã cho bằng:a) \(2\). b) \(3\). c) \( - 4\). d) \(0\).
Giá trị cực tiểu của hàm số đã cho bằng:a) \(2\). b) \(3\). c) \( - 4\). d) \(0\).
Phương pháp giải - Xem chi tiết
Dựa vào bảng biến thiên để nhận xét.
Lời giải chi tiết
Giá trị cực tiểu của hàm số là \(y = - 4 \Rightarrow C\)
Bài tập 2 trang 13 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và các phương pháp tính giới hạn thường gặp.
Bài tập 2 thường yêu cầu học sinh tính giới hạn của hàm số tại một điểm hoặc khi x tiến tới vô cùng. Các hàm số có thể là hàm đa thức, hàm hữu tỉ, hàm lượng giác hoặc các hàm số khác. Để giải bài tập, học sinh cần xác định đúng dạng của hàm số và áp dụng phương pháp tính giới hạn phù hợp.
Ví dụ: Tính giới hạn \lim_{x \to 2} \frac{x^2 - 4}{x - 2}
Giải:
Vậy, \lim_{x \to 2} \frac{x^2 - 4}{x - 2} = 4
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong SGK Toán 12 tập 1 - Cánh diều và các đề thi thử Toán 12.
Giải bài tập 2 trang 13 SGK Toán 12 tập 1 - Cánh diều đòi hỏi học sinh phải nắm vững kiến thức về giới hạn của hàm số và các phương pháp tính giới hạn. Bằng cách luyện tập thường xuyên và áp dụng các phương pháp giải phù hợp, các em có thể tự tin giải quyết các bài tập Toán 12 một cách hiệu quả.
| Phương pháp | Ứng dụng |
|---|---|
| Trực tiếp | Hàm số liên tục |
| Phân tích thành nhân tử | Hàm số hữu tỉ |
| Nhân liên hợp | Hàm số chứa căn thức |
| Quy tắc L'Hopital | Dạng vô định |