Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3, trang 24, 25 và 26 sách giáo khoa Toán 12 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Đường tiệm cận xiên
Trả lời câu hỏi Luyện tập 3 trang 25SGK Toán 12 Cánh diều
Chứng minh rằng đường thẳng \(y = - x\) là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}\).
Phương pháp giải:
Đưởng thẳng \(y = ax + b\left( {a \ne 0} \right)\) được gọi là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}} = - x + \frac{3}{{x + 2}}\).
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( { - x} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{3}{{x + 2}} = 0\).
Vậy đường thẳng \(y = - x\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}\)
Trả lời câu hỏi Luyện tập 4 trang 26SGK Toán 12 Cánh diều
Tìm tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\).
Phương pháp giải:
Đưởng thẳng \(y = ax + b\left( {a \ne 0} \right)\) được gọi là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}} = x - 6 + \frac{{20}}{{x + 3}}\).
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 6} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{20}}{{x + 3}} = 0\).
Vậy đường thẳng \(y = x - 6\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\)
Trả lời câu hỏi Hoạt động 3 trang 24SGK Toán 12 Cánh diều
Cho hàm số \(y = f\left( x \right) = x + 1 + \frac{1}{{x - 1}}\) có đồ thị \(\left( C \right)\) và đường thẳng \(y = x + 1\) (Hình 15). Tìm \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right];\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right]\)
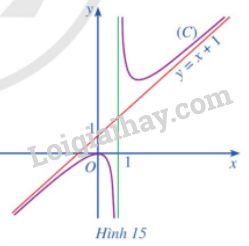
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 1}} = 0\\\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 1}} = 0\end{array} \right.\)
Trả lời câu hỏi Hoạt động 3 trang 24SGK Toán 12 Cánh diều
Cho hàm số \(y = f\left( x \right) = x + 1 + \frac{1}{{x - 1}}\) có đồ thị \(\left( C \right)\) và đường thẳng \(y = x + 1\) (Hình 15). Tìm \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right];\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right]\)
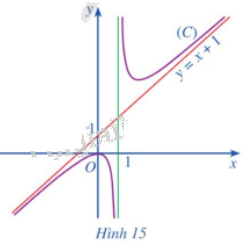
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 1}} = 0\\\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 1}} = 0\end{array} \right.\)
Trả lời câu hỏi Luyện tập 3 trang 25SGK Toán 12 Cánh diều
Chứng minh rằng đường thẳng \(y = - x\) là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}\).
Phương pháp giải:
Đưởng thẳng \(y = ax + b\left( {a \ne 0} \right)\) được gọi là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}} = - x + \frac{3}{{x + 2}}\).
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( { - x} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{3}{{x + 2}} = 0\).
Vậy đường thẳng \(y = - x\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}\)
Trả lời câu hỏi Luyện tập 4 trang 26SGK Toán 12 Cánh diều
Tìm tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\).
Phương pháp giải:
Đưởng thẳng \(y = ax + b\left( {a \ne 0} \right)\) được gọi là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}} = x - 6 + \frac{{20}}{{x + 3}}\).
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 6} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{20}}{{x + 3}} = 0\).
Vậy đường thẳng \(y = x - 6\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\)
Mục 3 trong SGK Toán 12 tập 1 - Cánh diều tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng, nền tảng cho việc học tập các kiến thức nâng cao hơn trong chương trình Toán 12. Việc nắm vững các khái niệm, định lý và kỹ năng giải bài tập trong mục này là vô cùng cần thiết.
Để giải tốt các bài tập trong Mục 3, các em cần:
Bài 1: Tính đạo hàm của hàm số f(x) = x2 + 3x - 2. Lời giải: f'(x) = 2x + 3.
Bài 2: Tính đạo hàm của hàm số g(x) = sin(x) + cos(x). Lời giải: g'(x) = cos(x) - sin(x).
Bài 3: Tìm đạo hàm của hàm số h(x) = ex + ln(x). Lời giải: h'(x) = ex + 1/x.
Bài 4: Cho hàm số y = x3 - 6x2 + 9x + 1. Tìm các điểm cực trị của hàm số. Lời giải: y' = 3x2 - 12x + 9. Giải phương trình y' = 0, ta được x = 1 và x = 3. Kiểm tra dấu của y' để xác định các điểm cực trị.
Bài 5: Lập bảng biến thiên của hàm số y = x4 - 4x2 + 3. Lời giải: Tính đạo hàm y' = 4x3 - 8x. Tìm các điểm cực trị và lập bảng biến thiên.
Bài 6: Giải phương trình đạo hàm f'(x) = 0 với f(x) = x2 - 4x + 5. Lời giải: f'(x) = 2x - 4. Giải phương trình 2x - 4 = 0, ta được x = 2.
Trong quá trình học và giải bài tập về đạo hàm, các em cần chú ý:
Hy vọng với những hướng dẫn chi tiết và lời giải bài tập trên, các em sẽ học tốt môn Toán 12 và đạt kết quả cao trong các kỳ thi.