Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2, trang 68, 69, 70 sách giáo khoa Toán 12 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Tọa độ của một vecto
Trả lời câu hỏi Hoạt động 3 trang 68 SGK Toán 12 Cánh diều
Cho điểm M trong không gian với hệ tọa độ Oxyz
a) Vẽ vecto \(\overrightarrow {OM} \)
b) Nêu cách xác định tọa độ của điểm M
Lời giải chi tiết:
a)
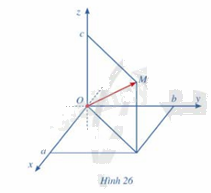
b) Nếu \(\;\overrightarrow {OM} \) có tọa độ (a;b;c) thì ta viết \(\;\overrightarrow {OM} \) = (a;b;c), trong đó a là hoành độ, b là tung độ và c là cao độ
Trả lời câu hỏi Hoạt động 4 trang 69 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho vecto \(\vec u\;\)(hình 28). Hãy xác định điểm A sao cho \(\overrightarrow {OA} = \vec u\)
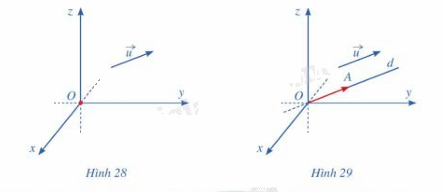
Phương pháp giải:
Vẽ \(\overrightarrow {OA\;} \)có tung độ, hoành độ và cao độ giống nhau
Lời giải chi tiết:
\(\overrightarrow {OA} = \vec u\)khicả hai có chung tung độ hoành độ và cao độ bằng nhau
Trả lời câu hỏi Hoạt động 5 trang 70 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho vecto \(\vec u = \left( {a;b;c} \right)\)( hình 31)
Lấy điểm A sao cho \(\overrightarrow {OA} = \vec u\).
a) Tìm hoành độ, tung độ và cao độ của điểm A
b) Biểu diễn vecto \(\overrightarrow {OH} \) qua vecto\(\;\vec i\) vecto \(\overrightarrow {OK} \) qua vecto \(\vec j\) ,vecto \(\overrightarrow {OP} \)qua vecto \(\vec k\)
c) Biểu diễn vecto \(\vec u\;\)theo các vecto \(\vec i,\vec j,\vec k\)
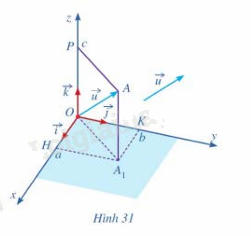
Phương pháp giải:
Áp dụng quy tắc các tọa độ của vecto
Lời giải chi tiết:
a)Ox là hoành độ của điểm A
Oy là tung dộ của điểm A
Oz là cao độ của điểm A
\(b)\overrightarrow {OH} = \overrightarrow {ai} \)
\(\overrightarrow {OK} = \overrightarrow {jb} \)
\(\overrightarrow {OP} = \overrightarrow {kc} \)
c)\(\vec u = \overrightarrow {OA} = \overrightarrow {OH} + \overrightarrow {OK} \)
=> \(\vec u = \overrightarrow {ai} + \overrightarrow {bj} \)
Trả lời câu hỏi Hoạt động 6 trang 71 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\)
a.Biểu diễn mỗi vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \) theo các vecto \(\overrightarrow i ,\overrightarrow j \) và \(\overrightarrow k \)
b. Tìm liên hệ giữa \(\overrightarrow {AB} \) và \(({x_B} - {x_A}).\vec i + ({y_B} - {y_A}).\vec j + ({z_B} - {z_A}).\vec k\)
c. Từ đó, tìm tọa độ vecto \(\overrightarrow {AB} \)
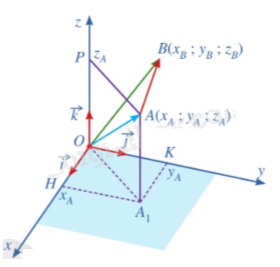
Phương pháp giải:
Sử dụng lý thuyết tọa độ của vecto trong không gian
Lời giải chi tiết:
a) \(\overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {OP} = \overrightarrow {OH} + \overrightarrow {OK} = {x_A}.\overrightarrow i + {y_A}.\overrightarrow j + {z_A}.\overrightarrow k \)
Tương tự, ta có: \(\overrightarrow {OB} = {x_B}.\overrightarrow i + {y_B}.\overrightarrow j + {z_B}.\overrightarrow k \)
b) Ta có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = {x_B}.\overrightarrow i + {y_B}.\overrightarrow j + {z_B}.\overrightarrow k - ({x_A}.\overrightarrow i + {y_A}.\overrightarrow j + {z_A}.\overrightarrow k ) = ({x_B} - {x_A}).\overrightarrow i + ({y_B} - {y_A}).\overrightarrow j + ({z_B} - {z_A}).\overrightarrow k \)
c)Tọa độ vecto \(\overrightarrow {AB} ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\)
Trả lời câu hỏi Hoạt động 3 trang 68 SGK Toán 12 Cánh diều
Cho điểm M trong không gian với hệ tọa độ Oxyz
a) Vẽ vecto \(\overrightarrow {OM} \)
b) Nêu cách xác định tọa độ của điểm M
Lời giải chi tiết:
a)
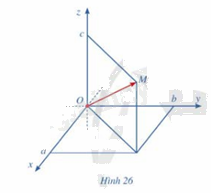
b) Nếu \(\;\overrightarrow {OM} \) có tọa độ (a;b;c) thì ta viết \(\;\overrightarrow {OM} \) = (a;b;c), trong đó a là hoành độ, b là tung độ và c là cao độ
Trả lời câu hỏi Hoạt động 4 trang 69 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho vecto \(\vec u\;\)(hình 28). Hãy xác định điểm A sao cho \(\overrightarrow {OA} = \vec u\)
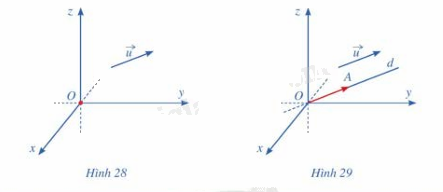
Phương pháp giải:
Vẽ \(\overrightarrow {OA\;} \)có tung độ, hoành độ và cao độ giống nhau
Lời giải chi tiết:
\(\overrightarrow {OA} = \vec u\)khicả hai có chung tung độ hoành độ và cao độ bằng nhau
Trả lời câu hỏi Hoạt động 5 trang 70 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho vecto \(\vec u = \left( {a;b;c} \right)\)( hình 31)
Lấy điểm A sao cho \(\overrightarrow {OA} = \vec u\).
a) Tìm hoành độ, tung độ và cao độ của điểm A
b) Biểu diễn vecto \(\overrightarrow {OH} \) qua vecto\(\;\vec i\) vecto \(\overrightarrow {OK} \) qua vecto \(\vec j\) ,vecto \(\overrightarrow {OP} \)qua vecto \(\vec k\)
c) Biểu diễn vecto \(\vec u\;\)theo các vecto \(\vec i,\vec j,\vec k\)
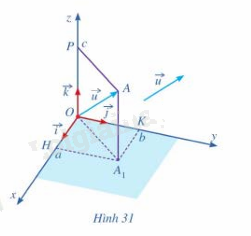
Phương pháp giải:
Áp dụng quy tắc các tọa độ của vecto
Lời giải chi tiết:
a)Ox là hoành độ của điểm A
Oy là tung dộ của điểm A
Oz là cao độ của điểm A
\(b)\overrightarrow {OH} = \overrightarrow {ai} \)
\(\overrightarrow {OK} = \overrightarrow {jb} \)
\(\overrightarrow {OP} = \overrightarrow {kc} \)
c)\(\vec u = \overrightarrow {OA} = \overrightarrow {OH} + \overrightarrow {OK} \)
=> \(\vec u = \overrightarrow {ai} + \overrightarrow {bj} \)
Trả lời câu hỏi Hoạt động 6 trang 71 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\)
a.Biểu diễn mỗi vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \) theo các vecto \(\overrightarrow i ,\overrightarrow j \) và \(\overrightarrow k \)
b. Tìm liên hệ giữa \(\overrightarrow {AB} \) và \(({x_B} - {x_A}).\vec i + ({y_B} - {y_A}).\vec j + ({z_B} - {z_A}).\vec k\)
c. Từ đó, tìm tọa độ vecto \(\overrightarrow {AB} \)
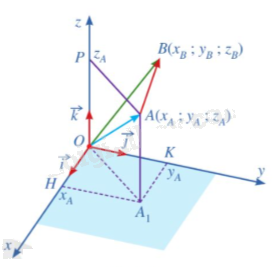
Phương pháp giải:
Sử dụng lý thuyết tọa độ của vecto trong không gian
Lời giải chi tiết:
a) \(\overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {OP} = \overrightarrow {OH} + \overrightarrow {OK} = {x_A}.\overrightarrow i + {y_A}.\overrightarrow j + {z_A}.\overrightarrow k \)
Tương tự, ta có: \(\overrightarrow {OB} = {x_B}.\overrightarrow i + {y_B}.\overrightarrow j + {z_B}.\overrightarrow k \)
b) Ta có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = {x_B}.\overrightarrow i + {y_B}.\overrightarrow j + {z_B}.\overrightarrow k - ({x_A}.\overrightarrow i + {y_A}.\overrightarrow j + {z_A}.\overrightarrow k ) = ({x_B} - {x_A}).\overrightarrow i + ({y_B} - {y_A}).\overrightarrow j + ({z_B} - {z_A}).\overrightarrow k \)
c)Tọa độ vecto \(\overrightarrow {AB} ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\)
Mục 2 của chương trình Toán 12 tập 1 - Cánh diều tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng, nền tảng cho việc học tập các kiến thức nâng cao hơn trong chương trình. Việc nắm vững các khái niệm, định lý và kỹ năng giải bài tập trong mục này là vô cùng cần thiết.
Bài tập này yêu cầu học sinh vận dụng các quy tắc tính đạo hàm cơ bản như quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp. Cần chú ý đến việc xác định đúng các hàm số thành phần và áp dụng quy tắc một cách chính xác.
Bài tập này yêu cầu học sinh tính đạo hàm bậc hai của hàm số, tức là đạo hàm của đạo hàm bậc nhất. Việc này đòi hỏi sự cẩn thận và chính xác trong các phép tính đạo hàm.
Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải các bài toán liên quan đến vận tốc, gia tốc, tối ưu hóa,... Đây là những bài toán có tính ứng dụng cao, giúp học sinh hiểu rõ hơn về ý nghĩa của đạo hàm trong thực tế.
Ví dụ: Một vật chuyển động với phương trình s(t) = t^3 - 6t^2 + 9t + 2 (s tính bằng mét, t tính bằng giây). Tìm vận tốc và gia tốc của vật tại thời điểm t = 2 giây.
| Hàm số | Đạo hàm |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = x^n | y' = nx^(n-1) |
| y = sin(x) | y' = cos(x) |
| y = cos(x) | y' = -sin(x) |
Để học tốt môn Toán 12, các em cần dành thời gian ôn tập lý thuyết, làm bài tập thường xuyên và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 68, 69, 70 SGK Toán 12 tập 1 - Cánh diều. Chúc các em học tập tốt!