Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài tập 3 trang 93 SGK Toán 12 tập 1 - Cánh diều một cách dễ dàng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Bảng 24 thống kê độ ẩm không khí tủng bình các tháng năm 2021 tại Đà Lạt và Vũng Tàu (đơn vị: %) a) Hãy lần lượt ghép các số liệu của Đà Lạt, Vũng Tàu thành năm nhóm sau: [75;78,3), [78,3;81,6), [81,6;84,9), [84,9;88,2),[88,2;91,5) b) Tính khoảng biến thiên, khoảng tứ phân vị, phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm của Đà Lạt và Vũng Tàu c) Trong hai thành phố Đà Lạt và Vũng Tàu, thành phố nào có độ ẩm không khí trung bình tháng đồng đều hơn?
Đề bài
Bảng 24 thống kê độ ẩm không khí tủng bình các tháng năm 2021 tại Đà Lạt và Vũng Tàu (đơn vị: %)
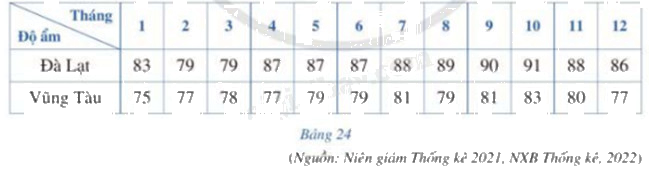
a) Hãy lần lượt ghép các số liệu của Đà Lạt, Vũng Tàu thành năm nhóm sau:
[75;78,3), [78,3;81,6), [81,6;84,9), [84,9;88,2),[88,2;91,5)
b) Tính khoảng biến thiên, khoảng tứ phân vị, phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm của Đà Lạt và Vũng Tàu
c) Trong hai thành phố Đà Lạt và Vũng Tàu, thành phố nào có độ ẩm không khí trung bình tháng đồng đều hơn?
Phương pháp giải - Xem chi tiết
Khoảng biến thiên là hiệu của đầu mút phải nhóm cuối cùng và đầu mút trái nhóm đầu tiên
Khoảng tứ phân vị là \({Q_3} - {Q_1}\)
Phương sai: \({s^2} = \frac{{{n_1}.{{({x_1} - \overline x )}^2} + {n_2}{{({x_2} - \overline x )}^2} + ... + {n_p}{{({x_p} - \overline x )}^2}}}{n}\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)
Thành phố nào có độ lệch chuẩn của nhiệt độ nhỏ hơn thì nhiệt độ không khí trung bình tháng đồng đều hơn
Lời giải chi tiết
a)
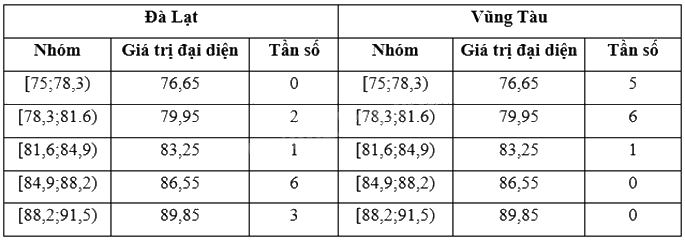
b) – Xét số liệu ở Đà Lạt:
+ Khoảng biến thiên: R = 91,5 – 75 = 16,5
+ Số phần tử của mẫu là n = 12
Tần số tích lũy của các nhóm lần lượt là \(c{f_1} = 0\), \(c{f_2} = 2\), \(c{f_3} = 3\), \(c{f_4} = 9\), \(c{f_5} = 12\)
Ta có: \(\frac{n}{4} = \frac{{12}}{4} = 3\) suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 3. Xét nhóm 3 là nhóm [81,6;84,9) có s = 81,6, h = 3,3, \({n_3} = 1\) và nhóm 2 là nhóm [78,3;81.6) có \(c{f_2} = 2\)
Ta có tứ phân vị thứ nhất là: \({Q_1} = s + \left( {\frac{{3 - c{f_2}}}{{{n_3}}}} \right).h = 81,6 + \left( {\frac{{3 - 2}}{1}} \right).3,3 = 84,9\)
Ta có: \(\frac{{3n}}{4} = \frac{{3.12}}{4} = 9\) suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 9. Xét nhóm 4 là nhóm [84,9;88,2) có t = 84,9, l = 3,3, \({n_4} = 6\) và nhóm 3 là nhóm [81,6;84,9) có \(c{f_3} = 3\)
Ta có tứ phân vị thứ ba là: \({Q_3} = t + \left( {\frac{{9 - c{f_3}}}{{{n_4}}}} \right).l = 84,9 + \left( {\frac{{9 - 3}}{6}} \right).3,3 = 88,2\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: \({Q_3} - {Q_1} = 88,2 - 84,9 = 3,3\)
+ Số trung bình cộng của mẫu số liệu ghép nhóm là: \(\overline {{x_1}} = \frac{{0.76,65 + 2.79,95 + 83,25 + 6.86,55 + 3.89,85}}{{12}} = 86\)
Phương sai của mẫu số liệu ghép nhóm là:
\({s_1}^2 = \frac{{0{{(76,65 - 86)}^2} + 2{{(79,95 - 86)}^2} + {{(83,25 - 86)}^2} + 6{{(86,55 - 86)}^2} + 3{{(89,95 - 86)}^2}}}{{12}} = 10,7825\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \({s_1} = \sqrt {{s_1}^2} = \sqrt {10,7825} \approx 3,28\)
– Xét số liệu ở Vũng Tàu:
+ Khoảng biến thiên: R = 91,5 - 75 = 16,5
+ Số phần tử của mẫu là n = 12
Tần số tích lũy của các nhóm lần lượt là \(c{f_1} = 5\), \(c{f_2} = 11\), \(c{f_3} = 12\), \(c{f_4} = 12\), \(c{f_5} = 12\)
Ta có: \(\frac{n}{4} = \frac{{12}}{4} = 3\) suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 3. Xét nhóm 1 là nhóm [75;78,3) có s = 75, h = 3,3, \({n_1} = 5\)
Ta có tứ phân vị thứ nhất là: \({Q_1} = s + \left( {\frac{{3 - c{f_0}}}{{{n_1}}}} \right).h = 75 + \left( {\frac{{3 - 0}}{5}} \right).3,3 = 76,98\)
Ta có: \(\frac{{3n}}{4} = \frac{{3.12}}{4} = 9\) suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 9. Xét nhóm 2 là nhóm [78,3;81,6) có t = 78,3, l = 3,3, \({n_2} = 6\) và nhóm 1 là nhóm [75;78,3) có \(c{f_1} = 5\)
Ta có tứ phân vị thứ ba là: \({Q_3} = t + \left( {\frac{{9 - c{f_1}}}{{{n_2}}}} \right).l = 75 + \left( {\frac{{9 - 5}}{6}} \right).3,3 = 77,2\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: \({Q_3} - {Q_1} = 77,2 - 76,98 = 0,22\)
+ Số trung bình cộng của mẫu số liệu ghép nhóm là: \(\overline {{x_2}} = \frac{{5.76,65 + 6.79,95 + 83,25}}{{12}} = 78,85\)
Phương sai của mẫu số liệu ghép nhóm là:
\({s_2}^2 = \frac{{5{{(76,65 - 78,85)}^2} + 6{{(79,95 - 78,85)}^2} + {{(83,25 - 78,85)}^2}}}{{12}} = 4,235\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \({s_2} = \sqrt {{s_2}^2} = \sqrt {4,235} \approx 2,06\)
c) Vũng Tàu có nhiệt độ không khí trung bình tháng đồng đều hơn vì độ lệch chuẩn nhỏ hơn
Bài tập 3 trang 93 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại vô cùng để giải quyết các bài toán cụ thể. Việc nắm vững các định nghĩa, tính chất và các phương pháp tính giới hạn là yếu tố then chốt để hoàn thành tốt bài tập này.
Bài tập 3 bao gồm các câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của hàm số tại một điểm hoặc tại vô cùng. Các hàm số thường gặp trong bài tập này là hàm đa thức, hàm hữu tỉ và các hàm số đặc biệt khác. Để giải quyết bài tập này, học sinh cần:
Để giải câu a, ta cần tính giới hạn của hàm số f(x) = (x^2 - 1) / (x - 1) khi x tiến tới 1. Ta có thể phân tích tử số thành (x - 1)(x + 1). Khi đó, giới hạn trở thành lim (x->1) (x + 1) = 2.
Đối với câu b, ta cần tính giới hạn của hàm số g(x) = (x^3 + 8) / (x + 2) khi x tiến tới -2. Tương tự như câu a, ta có thể phân tích tử số thành (x + 2)(x^2 - 2x + 4). Khi đó, giới hạn trở thành lim (x->-2) (x^2 - 2x + 4) = 12.
Câu c yêu cầu tính giới hạn của hàm số h(x) = (sqrt(x + 4) - 2) / x khi x tiến tới 0. Để giải quyết bài toán này, ta có thể nhân cả tử và mẫu với liên hợp của tử số, tức là (sqrt(x + 4) + 2). Khi đó, giới hạn trở thành lim (x->0) 1 / (sqrt(x + 4) + 2) = 1/4.
Trong quá trình giải bài tập về giới hạn, học sinh có thể sử dụng các phương pháp sau:
Để giải bài tập về giới hạn một cách hiệu quả, học sinh cần lưu ý những điều sau:
Để củng cố kiến thức về giới hạn, bạn có thể thử giải các bài tập sau:
Bài tập 3 trang 93 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính giới hạn. Hy vọng với những hướng dẫn chi tiết và các phương pháp giải quyết bài tập được trình bày trong bài viết này, bạn sẽ tự tin hơn trong việc học tập môn Toán.