Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 22, 23, 24 sách giáo khoa Toán 12 tập 1 - Cánh diều.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, khoa học, giúp các em nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
Đường tiệm cận đứng
Trả lời câu hỏi Luyện tập 2 trang 23SGK Toán 12 Cánh diều
Tìm tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + 3x}}{{x - 5}}\).
Phương pháp giải:
Đường thẳng \(x = {x_o}\) được gọi là đường tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
\(\mathop {\lim }\limits_{x \to x_o^ - } f\left( x \right) = + \infty \) ,\(\mathop {\lim }\limits_{x \to x_o^ - } f\left( x \right) = - \infty \),\(\mathop {\lim }\limits_{x \to x_o^ + } f\left( x \right) = + \infty \),\(\mathop {\lim }\limits_{x \to x_o^ + } f\left( x \right) = - \infty \).
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ 5 \right\}\).
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {5^ - }} y = \mathop {\lim }\limits_{x \to {5^ - }} \frac{{{x^2} + 3x}}{{x - 5}} = - \infty \\\mathop {\lim }\limits_{x \to {5^ + }} y = \mathop {\lim }\limits_{x \to {5^ + }} \frac{{{x^2} + 3x}}{{x - 5}} = + \infty \end{array} \right.\)
Vậy đường thẳng \(x = 5\) là tiệm cận đứng của đồ thị hàm số đã cho
Trả lời câu hỏi Hoạt động 2 trang 22 SGK Toán 12 Cánh diều
Cho hàm số \(y = f\left( x \right) = \frac{1}{x}\) có đồ thị là đường cong như Hình 12. Tìm \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)\)
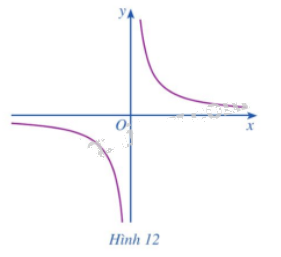
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = - \infty \).
Trả lời câu hỏi Luyện tập 2 trang 23SGK Toán 12 Cánh diều
Tìm tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + 3x}}{{x - 5}}\).
Phương pháp giải:
Đường thẳng \(x = {x_o}\) được gọi là đường tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
\(\mathop {\lim }\limits_{x \to x_o^ - } f\left( x \right) = + \infty \) ,\(\mathop {\lim }\limits_{x \to x_o^ - } f\left( x \right) = - \infty \),\(\mathop {\lim }\limits_{x \to x_o^ + } f\left( x \right) = + \infty \),\(\mathop {\lim }\limits_{x \to x_o^ + } f\left( x \right) = - \infty \).
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ 5 \right\}\).
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {5^ - }} y = \mathop {\lim }\limits_{x \to {5^ - }} \frac{{{x^2} + 3x}}{{x - 5}} = - \infty \\\mathop {\lim }\limits_{x \to {5^ + }} y = \mathop {\lim }\limits_{x \to {5^ + }} \frac{{{x^2} + 3x}}{{x - 5}} = + \infty \end{array} \right.\)
Vậy đường thẳng \(x = 5\) là tiệm cận đứng của đồ thị hàm số đã cho
Trả lời câu hỏi Hoạt động 2 trang 22 SGK Toán 12 Cánh diều
Cho hàm số \(y = f\left( x \right) = \frac{1}{x}\) có đồ thị là đường cong như Hình 12. Tìm \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)\)
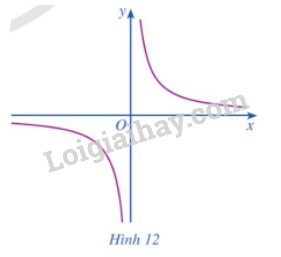
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = - \infty \).
Mục 2 trong SGK Toán 12 tập 1 - Cánh diều tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng trong chương trình Toán học, đặc biệt là trong việc học tập các kiến thức về đạo hàm và tích phân. Việc hiểu rõ về giới hạn hàm số sẽ giúp học sinh có thể giải quyết các bài toán phức tạp hơn một cách hiệu quả.
Mục 2 bao gồm các nội dung chính sau:
Trang 22 SGK Toán 12 tập 1 - Cánh diều chứa các bài tập vận dụng kiến thức về khái niệm giới hạn của hàm số tại một điểm. Các bài tập này yêu cầu học sinh phải hiểu rõ định nghĩa giới hạn và các tính chất của giới hạn để có thể giải quyết một cách chính xác.
Ví dụ, bài tập 1 yêu cầu tính giới hạn của hàm số f(x) = (x^2 - 1)/(x - 1) khi x tiến tới 1. Để giải bài tập này, ta có thể phân tích tử số thành nhân tử và rút gọn biểu thức, sau đó thay x = 1 vào biểu thức để tính giới hạn.
Trang 23 SGK Toán 12 tập 1 - Cánh diều tập trung vào các bài tập về giới hạn của hàm số tại vô cùng. Các bài tập này yêu cầu học sinh phải nắm vững các quy tắc tính giới hạn của các hàm số đa thức, hàm số phân thức khi x tiến tới vô cùng.
Ví dụ, bài tập 2 yêu cầu tính giới hạn của hàm số f(x) = (2x^2 + 1)/(x^2 + 3) khi x tiến tới vô cùng. Để giải bài tập này, ta có thể chia cả tử số và mẫu số cho x^2, sau đó tính giới hạn của biểu thức mới.
Trang 24 SGK Toán 12 tập 1 - Cánh diều chứa các bài tập tổng hợp về giới hạn hàm số, bao gồm cả các bài tập về giới hạn tại một điểm, giới hạn tại vô cùng và các dạng giới hạn đặc biệt. Các bài tập này yêu cầu học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết một cách hiệu quả.
Ví dụ, bài tập 3 yêu cầu tính giới hạn của hàm số f(x) = sin(x)/x khi x tiến tới 0. Đây là một dạng giới hạn đặc biệt, ta có thể sử dụng định lý giới hạn của sin(x)/x khi x tiến tới 0 để giải bài tập này.
Hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài tập về giới hạn hàm số trong Mục 2 SGK Toán 12 tập 1 - Cánh diều. Chúc các em học tập tốt!