Giải bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 1 - Cánh diều. Bài tập 13 trang 83 thuộc chương trình học quan trọng, đòi hỏi sự hiểu biết sâu sắc về kiến thức đã học.

Chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online tốt nhất, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài toán.

Xét hệ tọa độ Oxyz gắn với hình lập phương ABCD.A’B’C’D’ như Hình 39, đơn vị của mỗi trục bằng độ dài cạnh hình lập phương. Biết A(0;0;0), B(1;0;0), D(0;1;0), A’(0;0;1). a) Xác định tọa độ các đỉnh còn lại của hình lập phương ABCD.A’B’C’D’ b) Xác định tọa độ trọng tâm G của tam giác A’BD c) Xác định tọa độ các vecto \(\overrightarrow {OG} \) và \(\overrightarrow {OC'} \). Chứng minh rằng ba điểm O, G, C’ thẳng hàng và \(OG = \frac{1}{3}OC\)

Đề bài

Xét hệ tọa độ Oxyz gắn với hình lập phương ABCD.A’B’C’D’ như Hình 39, đơn vị của mỗi trục bằng độ dài cạnh hình lập phương. Biết A(0;0;0), B(1;0;0), D(0;1;0), A’(0;0;1).

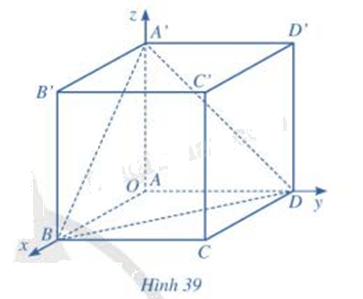
Giải bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều 1

a) Xác định tọa độ các đỉnh còn lại của hình lập phương ABCD.A’B’C’D’

b) Xác định tọa độ trọng tâm G của tam giác A’BD

c) Xác định tọa độ các vecto \(\overrightarrow {OG} \) và \(\overrightarrow {OC'} \). Chứng minh rằng ba điểm O, G, C’ thẳng hàng và \(OG = \frac{1}{3}OC\)

Phương pháp giải - Xem chi tiết Giải bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều 2

a) Quan sát hình vẽ

b) Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC

c) A, B, C thẳng hàng khi \(\overrightarrow {AB} = k\overrightarrow {AC} \)

Lời giải chi tiết

a) C(1;1;0); B’(1;0;1); C’(1;1;1); D’(0;1;1)

b) \(G(\frac{1}{3};\frac{1}{3};\frac{1}{3})\)

c) \(\overrightarrow {OG} = (\frac{1}{3};\frac{1}{3};\frac{1}{3})\)

\(\overrightarrow {OC'} = (1;1;1)\)

Ta có: \(\overrightarrow {OG} = \frac{1}{3}\overrightarrow {OC'} \) => O, G, C’ thẳng hàng

\(\left| {\overrightarrow {OG} } \right| = \frac{1}{3}\left| {\overrightarrow {OC'} } \right|\;\;hay\;\;OG = \frac{1}{3}OC\)

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều đặc sắc thuộc chuyên mục sgk toán 12 trên nền tảng học toán. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều: Tổng quan

Bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức này là nền tảng quan trọng cho việc học tập các chương trình Toán học nâng cao hơn.

Nội dung bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều

Bài tập 13 bao gồm các câu hỏi và bài tập liên quan đến:

Tính đạo hàm của hàm số tại một điểm.
Tìm đạo hàm của hàm số.
Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số.
Khảo sát hàm số bằng đạo hàm.

Phương pháp giải bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều

Để giải quyết hiệu quả các bài tập trong bài tập 13, học sinh cần:

Nắm vững các công thức tính đạo hàm cơ bản.
Hiểu rõ quy tắc tính đạo hàm của các hàm số hợp, hàm số lượng giác, hàm số mũ, hàm số logarit.
Vận dụng đạo hàm để giải quyết các bài toán thực tế.
Kiểm tra lại kết quả sau khi giải bài tập.

Lời giải chi tiết bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều

Dưới đây là lời giải chi tiết cho từng bài tập trong bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều:

Bài 1:

Cho hàm số f(x) = x³ - 3x² + 2. Tính f'(1).

Lời giải:

f'(x) = 3x² - 6x

f'(1) = 3(1)² - 6(1) = -3

Bài 2:

Tìm đạo hàm của hàm số y = sin(2x).

Lời giải:

y' = cos(2x) * 2 = 2cos(2x)

Bài 3:

Tìm phương trình tiếp tuyến của đồ thị hàm số y = x² tại điểm có hoành độ x = 2.

Lời giải:

y' = 2x

Tại x = 2, y = 2² = 4 và y' = 2(2) = 4

Phương trình tiếp tuyến là: y - 4 = 4(x - 2) => y = 4x - 4

Các dạng bài tập thường gặp trong bài tập 13

Ngoài các bài tập cơ bản về tính đạo hàm, bài tập 13 còn có thể xuất hiện các dạng bài tập sau:

Bài tập về đạo hàm của hàm số ẩn.
Bài tập về đạo hàm cấp hai.
Bài tập về ứng dụng đạo hàm để tìm cực trị của hàm số.

Mẹo giải bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều

Để giải bài tập 13 một cách hiệu quả, bạn có thể áp dụng các mẹo sau:

Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Sử dụng các công thức tính đạo hàm một cách chính xác.
Kiểm tra lại kết quả sau khi giải bài tập.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.

Tài liệu tham khảo

Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:

Sách giáo khoa Toán 12 tập 1 - Cánh diều.
Sách bài tập Toán 12 tập 1 - Cánh diều.
Các trang web học toán online uy tín.

Kết luận

Bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng, giúp học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và các phương pháp giải bài tập được trình bày ở trên, bạn sẽ tự tin giải quyết các bài toán trong bài tập này và đạt kết quả tốt trong môn Toán.