Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1, trang 15, 16, 17 sách giáo khoa Toán 12 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Định nghĩa
Trả lời câu hỏi Luyện tập 1 trang 16 SGK Toán 12 Cánh diều
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(f\left( x \right) = \sqrt {9 - {x^2}} \) trên đoạn \(\left[ { - 3;3} \right]\).
Phương pháp giải:
Đánh giá dựa vào điều kiện xác định của x.
Lời giải chi tiết:
Ta có: \(x \in \left[ { - 3;3} \right] \Rightarrow 0 \le {x^2} \le 9 \Rightarrow 0 \le 9 - {x^2} \le 9 \Rightarrow 0 \le \sqrt {9 - {x^2}} \le 3\).
Vậy \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 3 \Leftrightarrow x = 0\\\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 0 \Leftrightarrow x = \pm 3\end{array} \right.\).
Trả lời câu hỏi Hoạt động 1 trang 15 SGK Toán 12 Cánh diều
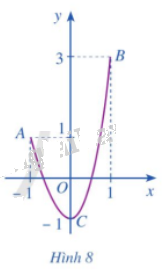
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;1} \right]\) và có đồ thị là đường cong ở Hình 8. Quan sát đồ thị và cho biết:
a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất
b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất
Lời giải chi tiết:
a) Điểm B là điểm thuộc đồ thị hàm số có tung độ lớn nhất
b) Điểm C là điểm thuộc đồ thị hàm số có tung độ nhỏ nhất
Trả lời câu hỏi Hoạt động 1 trang 15 SGK Toán 12 Cánh diều
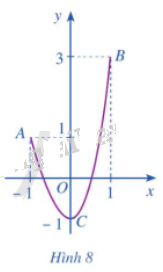
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;1} \right]\) và có đồ thị là đường cong ở Hình 8. Quan sát đồ thị và cho biết:
a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất
b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất
Lời giải chi tiết:
a) Điểm B là điểm thuộc đồ thị hàm số có tung độ lớn nhất
b) Điểm C là điểm thuộc đồ thị hàm số có tung độ nhỏ nhất
Trả lời câu hỏi Luyện tập 1 trang 16 SGK Toán 12 Cánh diều
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(f\left( x \right) = \sqrt {9 - {x^2}} \) trên đoạn \(\left[ { - 3;3} \right]\).
Phương pháp giải:
Đánh giá dựa vào điều kiện xác định của x.
Lời giải chi tiết:
Ta có: \(x \in \left[ { - 3;3} \right] \Rightarrow 0 \le {x^2} \le 9 \Rightarrow 0 \le 9 - {x^2} \le 9 \Rightarrow 0 \le \sqrt {9 - {x^2}} \le 3\).
Vậy \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 3 \Leftrightarrow x = 0\\\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 0 \Leftrightarrow x = \pm 3\end{array} \right.\).
Mục 1 của SGK Toán 12 tập 1 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số và đồ thị. Đây là nền tảng quan trọng cho các kiến thức nâng cao hơn trong chương trình học. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức về tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số, và vẽ đồ thị hàm số.
Bài 1 thường yêu cầu học sinh xác định tập xác định của hàm số. Để giải bài này, học sinh cần nắm vững các điều kiện để hàm số có nghĩa, ví dụ như mẫu số khác 0, biểu thức dưới dấu căn lớn hơn hoặc bằng 0, và logarit có cơ số lớn hơn 0 và khác 1.
Bài 2 thường liên quan đến việc xét tính đơn điệu của hàm số. Học sinh cần sử dụng đạo hàm để xác định dấu của đạo hàm trên các khoảng xác định. Nếu đạo hàm dương trên một khoảng, hàm số đồng biến trên khoảng đó. Nếu đạo hàm âm trên một khoảng, hàm số nghịch biến trên khoảng đó.
Bài 3 thường yêu cầu tìm cực trị của hàm số. Học sinh cần giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị. Sau đó, sử dụng dấu của đạo hàm để xác định loại cực trị (cực đại hoặc cực tiểu).
Bài 4 thường yêu cầu vẽ đồ thị hàm số. Học sinh cần xác định các yếu tố quan trọng của đồ thị như tập xác định, tập giá trị, điểm đồng biến, điểm nghịch biến, cực trị, và giao điểm với các trục tọa độ. Sau đó, vẽ đồ thị dựa trên các yếu tố này.
Ví dụ: Giải phương trình đạo hàm f'(x) = 0 để tìm điểm cực trị của hàm số f(x) = x3 - 3x2 + 2.
f'(x) = 3x2 - 6x = 0
3x(x - 2) = 0
Vậy x = 0 hoặc x = 2.
Để xác định loại cực trị, ta xét dấu của f'(x) trên các khoảng (-∞, 0), (0, 2), và (2, +∞).
Kết luận: Hàm số có cực đại tại x = 0 và cực tiểu tại x = 2.
Hãy dành thời gian ôn tập lý thuyết và làm bài tập một cách cẩn thận. Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè. Chúc các em học tốt!
| Công thức | Mô tả |
|---|---|
| Đạo hàm của xn | nxn-1 |
| Đạo hàm của sin(x) | cos(x) |
| Đạo hàm của cos(x) | -sin(x) |