Giải mục 4 trang 79,80 SGK Toán 12 tập 1 - Cánh diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 79,80 SGK Toán 12 tập 1 - Cánh diều trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi luôn cố gắng mang đến những bài giải chất lượng nhất, đáp ứng nhu cầu học tập của các em.

Cách tìm tọa độ của một vecto vuông góc với hai vecto cho trước

Đề bài

Trả lời câu hỏi Hoạt động 4 trang 79 SGK Toán 12 Cánh diều

a) Cho hình lập phương ABCD.A’B’C’D’ có A(0;0;0), B(1;0;0), D(0;1;0), C’(1;1;1). Hãy chỉ ra tọa độ của một vecto vuông góc với cả hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \)

b) Cho hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) không cùng phương. Xét vecto \(\overrightarrow w = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\).

Tính \(\overrightarrow w .\overrightarrow u \), \(\overrightarrow w .\overrightarrow v \)
Vecto \(\overrightarrow w \) có vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) hay không?

Phương pháp giải - Xem chi tiết Giải mục 4 trang 79,80 SGK Toán 12 tập 1 - Cánh diều 1

Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có biểu thức tọa độ của tích vô hướng \(\overrightarrow a .\overrightarrow b = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}\) và \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\)

Lời giải chi tiết

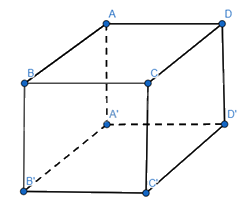
Giải mục 4 trang 79,80 SGK Toán 12 tập 1 - Cánh diều 2

Ta có: \(\overrightarrow {AB} = (1;0;0)\), \(\overrightarrow {AD} = (0;1;0)\)

\(A'(0;0;1) \Rightarrow \overrightarrow {AA'} = (0;0;1)\)

Ta có: \(\overrightarrow {AA'} .\overrightarrow {AB} = 0.1 + 0.0 + 1.0 = 0 \Leftrightarrow \overrightarrow {AA'} \bot \overrightarrow {AB} \)

\(\overrightarrow {AA'} .\overrightarrow {AD} = 0.0 + 0.1 + 1.0 = 0 \Leftrightarrow \overrightarrow {AA'} \bot \overrightarrow {AD} \)

Vậy \(\overrightarrow {AA'} \) vuông góc với cả hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \)

b) \(\overrightarrow w .\overrightarrow u = ({y_1}{z_2} - {y_2}{z_1}){x_1} + ({z_1}{x_2} - {z_2}{x_1}){y_1} + ({x_1}{y_2} - {x_2}{y_1}){z_1} = {x_1}{y_1}{z_2} - {x_1}{y_2}{z_1} + {y_1}{z_1}{x_2} - {y_1}{z_2}{x_1} + {z_1}{x_1}{y_2} - {z_1}{x_2}{y_1} = 0\)

\(\overrightarrow w .\overrightarrow v = ({y_1}{z_2} - {y_2}{z_1}){x_2} + ({z_1}{x_2} - {z_2}{x_1}){y_2} + ({x_1}{y_2} - {x_2}{y_1}){z_2} = {x_2}{y_1}{z_2} - {x_2}{y_2}{z_1} + {y_2}{z_1}{x_2} - {y_2}{z_2}{x_1} + {z_2}{x_1}{y_2} - {z_2}{x_2}{y_1} = 0\)

Vecto \(\overrightarrow w \) có vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \)

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải mục 4 trang 79,80 SGK Toán 12 tập 1 - Cánh diều đặc sắc thuộc chuyên mục toán lớp 12 trên nền tảng soạn toán. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải mục 4 trang 79,80 SGK Toán 12 tập 1 - Cánh diều: Tổng quan

Mục 4 trong SGK Toán 12 tập 1 - Cánh diều tập trung vào việc nghiên cứu về đạo hàm của hàm số. Đây là một phần kiến thức nền tảng và quan trọng trong chương trình Toán học lớp 12, đóng vai trò then chốt trong việc giải quyết các bài toán liên quan đến cực trị, đơn điệu của hàm số và ứng dụng của đạo hàm trong các lĩnh vực khác.

Nội dung chính của Mục 4

Mục 4 bao gồm các nội dung chính sau:

Định nghĩa đạo hàm: Giới thiệu khái niệm đạo hàm của hàm số tại một điểm và trên một khoảng.
Quy tắc tính đạo hàm: Trình bày các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, cũng như đạo hàm của hàm hợp.
Đạo hàm của các hàm số thường gặp: Cung cấp công thức tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.
Ứng dụng của đạo hàm: Giới thiệu các ứng dụng của đạo hàm trong việc tìm cực trị, xét tính đơn điệu của hàm số và giải các bài toán thực tế.

Giải chi tiết bài tập mục 4 trang 79,80

Dưới đây là lời giải chi tiết các bài tập trong mục 4 trang 79,80 SGK Toán 12 tập 1 - Cánh diều:

Bài 1: Tính đạo hàm của các hàm số sau

a) y = x³ - 2x² + 5x - 1

Lời giải: y' = 3x² - 4x + 5

b) y = sin(2x) + cos(x)

Lời giải: y' = 2cos(2x) - sin(x)

Bài 2: Tìm đạo hàm của hàm số y = (x² + 1) / (x - 1)

Lời giải: Sử dụng quy tắc đạo hàm của thương, ta có:

y' = [(2x)(x - 1) - (x² + 1)(1)] / (x - 1)² = (x² - 2x - 1) / (x - 1)²

Bài 3: Cho hàm số y = f(x) = x². Tính f'(2)

Lời giải: f'(x) = 2x. Do đó, f'(2) = 2 * 2 = 4

Phương pháp giải bài tập đạo hàm hiệu quả

Để giải các bài tập về đạo hàm một cách hiệu quả, các em cần nắm vững các kiến thức sau:

Nắm vững định nghĩa và các quy tắc tính đạo hàm: Đây là nền tảng cơ bản để giải quyết mọi bài toán về đạo hàm.
Thành thạo các công thức đạo hàm của các hàm số thường gặp: Việc nhớ và áp dụng đúng các công thức sẽ giúp các em tiết kiệm thời gian và tránh sai sót.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp các em hiểu sâu hơn về kiến thức và rèn luyện kỹ năng giải bài tập.
Sử dụng các công cụ hỗ trợ: Các công cụ tính đạo hàm online có thể giúp các em kiểm tra lại kết quả và hiểu rõ hơn về quá trình tính đạo hàm.

Ứng dụng của đạo hàm trong thực tế

Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:

Vật lý: Tính vận tốc, gia tốc của vật chuyển động.
Kinh tế: Tính chi phí biên, doanh thu biên, lợi nhuận biên.
Kỹ thuật: Tối ưu hóa thiết kế, điều khiển hệ thống.

Kết luận

Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ nắm vững kiến thức về đạo hàm và tự tin hơn trong quá trình học tập môn Toán 12. Chúc các em học tốt!