Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 1 - Cánh diều. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài tập 5 trang 64, từ đó nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất, kèm theo các ví dụ minh họa cụ thể để bạn có thể áp dụng vào các bài tập tương tự.
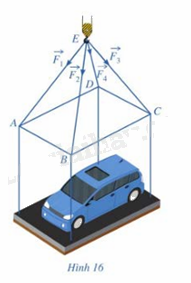
Một chiếc oto được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hinhg chữ nhật ABCD, mặt phẳng (ABCD) song song với mặt phẳng nằm ngang . Khung sắt có được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng 60(^circ )( hình 16 ). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Tính trọng lượng của chiếc xe oto ( làm tròn đến hàng đơn vị), biết rằng các lực căng
Đề bài
Một chiếc oto được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hinhg chữ nhật ABCD, mặt phẳng (ABCD) song song với mặt phẳng nằm ngang . Khung sắt có được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng 60\(^\circ \)( hình 16 ). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Tính trọng lượng của chiếc xe oto ( làm tròn đến hàng đơn vị), biết rằng các lực căng \(\overrightarrow {{F_1},} \overrightarrow {{F_2},} \overrightarrow {{F_3},} \overrightarrow {{F_4}} \) đều có cường độ là 4700N và trọng lượng của khung sắt là 3000N.
Phương pháp giải - Xem chi tiết
Có F1,2,3,4, tính F hợp lực.
Lấy F trừ trọng lực của khung (p) => trọng lực của xe rồi tính trọng lượng xe.
Lời giải chi tiết
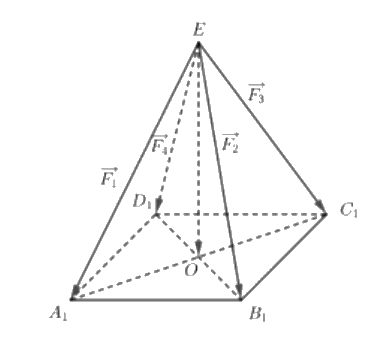
Gọi \({A_1},{B_1},{C_1},{D_1}\) lần lượt là các điểm sao cho \(\overrightarrow {E{A_1}} = \overrightarrow {{F_1}} ,\overrightarrow {E{B_1}} = \overrightarrow {{F_2}} ,\overrightarrow {E{C_1}} = \overrightarrow {{F_3}} ,\overrightarrow {E{D_1}} = \overrightarrow {{F_4}} \).
Vì EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng \({60^o}\) nê \(E{A_1},E{B_1},E{C_1},E{D_1}\) bằng nhau và cùng tạo với mặt phẳng \(({A_1}{B_1}{C_1}{D_1})\) một góc bằng \({60^o}\).
Vì ABCD là hình chữ nhật nên \({A_1}{B_1}{C_1}{D_1}\) cũng là hình chữ nhật.
Gọi O là tâm của hình chữ nhật \({A_1}{B_1}{C_1}{D_1}\).
Do đó, góc giữa đường thẳng \(E{A_1}\) và mặt phẳng \(({A_1}{B_1}{C_1}{D_1})\) bằng \(\widehat {E{A_1}O}\).
Suy ra \(\widehat {E{A_1}O} = {60^o}\).
Ta có \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_4}} } \right| = 4700\) (N) nên \(E{A_1} = E{B_1} = E{C_1} = E{D_1} = 4700\).
Tam giác \(E{A_1}O\) vuông tại O nên \(OE = E{A_1}\sin \widehat {E{A_1}O} = 4700\sin {60^o} = 2350\sqrt 3 \).
Theo quy tắc ba điểm, ta có \(\overrightarrow {E{A_1}} = \overrightarrow {EO} + \overrightarrow {O{A_1}} ,\overrightarrow {E{B_1}} = \overrightarrow {EO} + \overrightarrow {O{B_1}} ,\overrightarrow {E{C_1}} = \overrightarrow {EO} + \overrightarrow {O{C_1}} ,\overrightarrow {E{D_1}} = \overrightarrow {EO} + \overrightarrow {O{D_1}} \).
Vì O là trung điểm của \({A_1}{C_1}\) và \({B_1}{D_1}\) nên \(\overrightarrow {O{A_1}} + \overrightarrow {O{C_1}} = \overrightarrow 0 ,\overrightarrow {O{B_1}} + \overrightarrow {O{D_1}} = \overrightarrow 0 \).
Từ đó suy ra \(\overrightarrow {E{A_1}} + \overrightarrow {E{B_1}} + \overrightarrow {E{C_1}} + \overrightarrow {E{D_1}} = 4\overrightarrow {EO} \).
Do đó \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} = 4\overrightarrow {EO} \).
Vì chiếc khung sắt chứa xe ô tô ở vị trí cân bằng nên \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} = \overrightarrow P \), ở đó \(\overrightarrow P \) là trọng lực tác dụng lên khung sắt chứa xe ô tô.
Suy ra trọng lượng của khung sắt chứa chiếc xe ô tô là \(\left| {\overrightarrow P } \right| = 4\left| {\overrightarrow {EO} } \right| = 4.2350\sqrt 3 = 9400\sqrt 3 \) (N).
Vì trọng lượng của khung sắt là 3 000 N nên trọng lượng của chiếc xe ô tô là \(9400\sqrt 3 - 3000 \approx 13281\) (N).
Bài tập 5 trang 64 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại vô cùng để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và định lý liên quan là yếu tố then chốt để hoàn thành bài tập này một cách hiệu quả.
Bài tập 5 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của hàm số tại một điểm hoặc tại vô cùng. Các hàm số được sử dụng trong bài tập có thể là hàm đa thức, hàm hữu tỉ, hoặc các hàm số phức tạp hơn. Để giải quyết bài tập này, học sinh cần:
Để giải câu a, ta cần tính giới hạn của hàm số f(x) khi x tiến tới 2. Ta có:
lim (x→2) (x^2 - 4) / (x - 2)
Ta có thể phân tích tử số thành (x - 2)(x + 2). Khi đó:
lim (x→2) (x - 2)(x + 2) / (x - 2) = lim (x→2) (x + 2) = 4
Vậy, giới hạn của hàm số tại x = 2 là 4.
Để giải câu b, ta cần tính giới hạn của hàm số f(x) khi x tiến tới vô cùng. Ta có:
lim (x→∞) (2x^2 + 1) / (x^2 + 3)
Ta có thể chia cả tử số và mẫu số cho x^2. Khi đó:
lim (x→∞) (2 + 1/x^2) / (1 + 3/x^2) = 2 / 1 = 2
Vậy, giới hạn của hàm số tại vô cùng là 2.
Câu c tương tự như câu a và b, yêu cầu học sinh áp dụng các quy tắc tính giới hạn để tìm ra kết quả.
Ngoài bài tập 5, còn rất nhiều bài tập tương tự về giới hạn hàm số trong SGK Toán 12 tập 1 - Cánh diều. Để giải quyết các bài tập này, học sinh cần nắm vững các phương pháp sau:
Khi giải bài tập về giới hạn hàm số, học sinh cần lưu ý những điều sau:
Bài tập 5 trang 64 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn hàm số. Hy vọng rằng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài tập tương tự.