Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 1 - Cánh diều. Bài viết này sẽ giúp bạn hiểu rõ phương pháp giải bài tập 4 trang 43, từ đó nâng cao kiến thức và kỹ năng giải toán của mình.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tự tin chinh phục môn Toán.
Đường cong ở hình 30 là đồ thị của hàm số:
Đề bài
Đường cong ở hình 30 là đồ thị của hàm số:
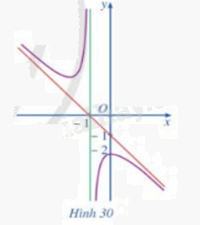
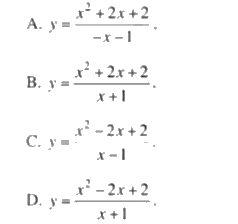
Phương pháp giải - Xem chi tiết
Xét tiệm cận xiên của đồ thị
Xét các hàm số
Lời giải chi tiết
Vì đồ thị hàm số đi qua (0:2)
=> Loại B,D
Vì hàm số có tcd là x=-1
=>\(\mathop {\lim }\limits_{\;x \to - 1} f\left( x \right) = \infty \)
Xét a, \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 2}}{{ - x - 1}} = \mathop {\lim }\limits_{ - x - 1} ( - x - 1 - \frac{1}{{x + 1}}) = - \infty \)
=> Chọn A
Bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể. Việc nắm vững lý thuyết và kỹ năng giải bài tập này là rất quan trọng để học tốt các kiến thức tiếp theo trong chương trình Toán 12.
Bài tập 4 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của hàm số tại một điểm cho trước. Các hàm số có thể là hàm đa thức, hàm hữu tỉ, hoặc các hàm số khác. Để giải quyết bài tập này, học sinh cần:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh diều:
Để tính giới hạn của hàm số tại một điểm, ta có thể sử dụng phương pháp thay trực tiếp giá trị của điểm đó vào hàm số. Nếu kết quả là một số thực, thì đó là giới hạn của hàm số tại điểm đó. Nếu kết quả là một biểu thức không xác định, ta cần sử dụng các kỹ thuật biến đổi đại số để đơn giản hóa biểu thức và tìm ra giới hạn.
Ví dụ, nếu hàm số là f(x) = (x^2 - 1) / (x - 1), và ta muốn tính giới hạn của hàm số tại x = 1, ta không thể thay trực tiếp x = 1 vào hàm số vì mẫu số sẽ bằng 0. Thay vào đó, ta có thể phân tích tử số thành (x - 1)(x + 1), và rút gọn biểu thức thành f(x) = x + 1. Sau đó, ta có thể thay x = 1 vào biểu thức rút gọn để tìm ra giới hạn, là 2.
Tương tự như câu a, ta cần xác định đúng dạng hàm số và phương pháp tính giới hạn phù hợp. Nếu hàm số là hàm hữu tỉ, ta cần kiểm tra xem mẫu số có bằng 0 tại điểm cần tính giới hạn hay không. Nếu mẫu số bằng 0, ta cần sử dụng các kỹ thuật biến đổi đại số để đơn giản hóa biểu thức và tìm ra giới hạn.
Đối với các hàm số phức tạp hơn, ta có thể cần sử dụng các định lý về giới hạn, chẳng hạn như định lý kẹp, hoặc các kỹ thuật khác để tìm ra giới hạn.
Ngoài bài tập 4 trang 43, SGK Toán 12 tập 1 - Cánh diều còn có nhiều bài tập tương tự về giới hạn của hàm số. Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Để củng cố kiến thức và kỹ năng giải bài tập về giới hạn của hàm số, học sinh nên luyện tập thêm các bài tập trong SGK, sách bài tập, và các đề thi thử. Ngoài ra, học sinh cũng có thể tìm kiếm các tài liệu học tập trực tuyến, chẳng hạn như các video bài giảng, các bài viết hướng dẫn, và các bài tập trắc nghiệm.
Bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ về giới hạn của hàm số. Việc nắm vững kiến thức và kỹ năng giải bài tập này là rất quan trọng để học tốt các kiến thức tiếp theo trong chương trình Toán 12. Hy vọng rằng, với lời giải chi tiết và các hướng dẫn trong bài viết này, bạn sẽ tự tin chinh phục bài tập này và đạt kết quả tốt trong môn Toán.