Chào mừng các em học sinh đến với lời giải chi tiết bài tập 5 trang 103 SGK Toán 12 tập 2 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 12.
Bài tập 5 thuộc chương trình học Toán 12 tập 2, tập trung vào các kiến thức về tích phân.
Giả sử trong một nhóm người có 2 người nhiễm bệnh, 58 người còn lại là không nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 85%, nhưng đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 7%. a) Vẽ sơ đồ hình cây biểu thị tình huống trên. b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất đ
Đề bài
Giả sử trong một nhóm người có 2 người nhiễm bệnh, 58 người còn lại là không nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 85%, nhưng đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 7%.
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất để X là người nhiễm bệnh.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định nghĩa xác suất có điều kiện để tính: Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, kí hiệu là P(A|B). Nếu \(P\left( B \right) > 0\) thì \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\).
Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Sử dụng kiến thức về sơ đồ hình cây để tính.
Lời giải chi tiết
a) Xét hai biến cố: A: “Người được chọn bị nhiễm bệnh”; B: “Người được chọn có phản ứng dương tính”.
Vì trong nhóm có 2 người nhiễm bệnh và 58 người còn lại không nhiễm bệnh nên \(P\left( A \right) = \frac{1}{{30}},P\left( {\overline A } \right) = \frac{{29}}{{30}}\).
Vì đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 85%, nhưng đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 7% nên \(P\left( {B|A} \right) = 0,85;P\left( {B|\overline A } \right) = 0,07\).
Sơ đồ cây biểu thị tình huống đã cho như sau:
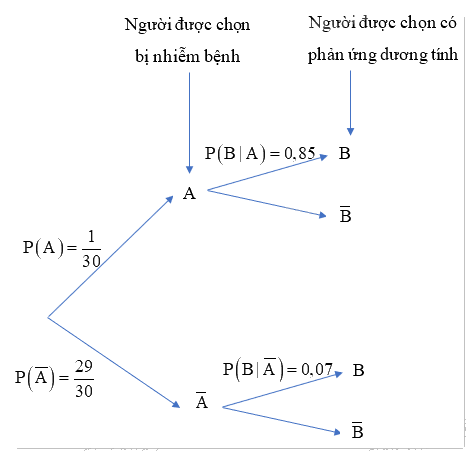
b) Ta có: \(P\left( {A|B} \right) = \frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( B \right)}} = \frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right)}}\)
\( = \frac{{\frac{1}{{30}}.0,85}}{{\frac{1}{{30}}.0,85 + \frac{{29}}{{30}}.0,07}} = \frac{{85}}{{288}} \approx 0,295\).
Vậy xác suất để X là người nhiễm bệnh là 0,295.
Bài tập 5 trang 103 SGK Toán 12 tập 2 - Cánh diều yêu cầu học sinh vận dụng kiến thức về tích phân để giải quyết các bài toán thực tế. Bài tập này thường liên quan đến việc tính diện tích hình phẳng, thể tích vật thể, hoặc các ứng dụng khác của tích phân trong các lĩnh vực khoa học và kỹ thuật.
Bài tập 5 thường bao gồm các dạng bài sau:
Để giải bài tập 5 trang 103 SGK Toán 12 tập 2 - Cánh diều một cách hiệu quả, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Ví dụ 1: Tính tích phân \int_0^1 x^2 dx
Lời giải:
Sử dụng công thức tích phân của hàm số lũy thừa, ta có:
\int_0^1 x^2 dx = \frac{x^3}{3} \Big|_0^1 = \frac{1^3}{3} - \frac{0^3}{3} = \frac{1}{3}
Ví dụ 2: Tính diện tích hình phẳng giới hạn bởi đường cong y = x^2 và trục Ox trên đoạn [0, 2]
Lời giải:
Diện tích hình phẳng được tính bằng tích phân:
S = \int_0^2 x^2 dx = \frac{x^3}{3} \Big|_0^2 = \frac{2^3}{3} - \frac{0^3}{3} = \frac{8}{3}
Ngoài SGK Toán 12 tập 2 - Cánh diều, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải bài tập:
Bài tập 5 trang 103 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về tích phân và rèn luyện kỹ năng giải toán. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ tự tin giải quyết bài tập này một cách hiệu quả.