Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 11 trang 80 SGK Toán 12 tập 2 theo chương trình Cánh diều.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn nắm vững kiến thức Toán học.
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí \(A\left( {3,5; - 2;0,4} \right)\) và sẽ hạ cánh ở vị trí \[B\left( {3,5;5,5;0} \right)\] trên đường băng EG (Hình 37).
Đề bài
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí \(A\left( {3,5; - 2;0,4} \right)\) và sẽ hạ cánh ở vị trí \(B\left( {3,5;5,5;0} \right)\) trên đường băng EG (Hình 37).
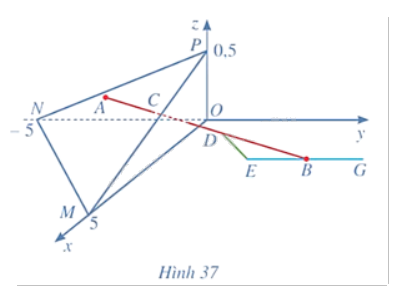
a) Viết phương trình đường thẳng AB.
b) Hãy cho biết góc trượt (góc giữa đường bay AB và mặt phẳng nằm ngang (Oxy)) có nằm trong phạm vi cho phép từ \(2,{5^o}\) đến \(3,{5^o}\) hay không.
c) Có một lớp mây được mô phỏng bởi một mặt phẳng \(\left( \alpha \right)\) đi qua ba điểm M(5; 0; 0), N(0; -5; 0), P(0; 0; 0,5). Tìm tọa độ của điểm C là vị trí mà máy bay xuyên qua đám mây để hạ cánh.
d) Tìm tọa độ của điểm D trên đoạn thẳng AB là vị trí mà máy bay ở độ cao 120m.
e) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu E(3,5; 6,5; 0) của đường băng ở độ cao tối thiểu là 120m. Hỏi sau khi ra khỏi đám mây, người phi công có đạt được quy định an toàn đó hay không? Biết rằng tầm nhìn của người phi công sau khi ra khỏi đám mây là 900m (Nguồn: R.Larson and B.Edwards, Calculus 10e, Cengage, 2014).
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về phương trình tham số của đường thẳng để viết phương trình tham số đường thẳng: Hệ phương trình \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\), trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
b) Sử dụng kiến thức về côsin góc giữa đường thẳng và mặt phẳng để tính: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( {{a_1};{b_1};{c_1}} \right)\) và mặt phẳng (P) có vectơ pháp tuyến
\(\overrightarrow n = \left( {{a_2};{b_2};{c_2}} \right)\). Gọi \(\left( {\Delta ,\left( P \right)} \right)\) là góc giữa đường thẳng \(\Delta \) và mặt phẳng (P). Khi đó, \(\sin \left( {\Delta ,\left( P \right)} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right| = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\).
c)
+ Viết phương trình mặt phẳng (MNP) đi qua điểm M và nhận \(\left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right]\) làm một vectơ pháp tuyến.
+ Vì C thuộc đường thẳng AB nên tính tọa độ điểm C theo t.
+ Thay tọa độ điểm C (theo ẩn t) vào phương trình mặt phẳng (MNP) ta tìm được t. Từ đó tính được tọa độ điểm C.
d) Sử dụng kiến thức khoảng cách từ một điểm đến một mặt phẳng để tính: Khoảng cách từ điểm \({M_o}\left( {{x_o};{y_o},{z_o}} \right)\) đến mặt phẳng (P): \(Ax + By + Cz + D = 0\left( {{A^2} + {B^2} + {C^2} > 0} \right)\) được tính theo công thức: \(d\left( {{M_o},\left( P \right)} \right) = \frac{{\left| {A{x_o} + B{y_o} + C{z_o} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)
e) Tính DE, so sánh DE với 900m, từ đó đưa ra kết luận.
Lời giải chi tiết
a) Đường thẳng AB đi qua điểm \(A\left( {3,5; - 2;0,4} \right)\) và nhận \(\overrightarrow {AB} = \left( {0;7,5; - 0,4} \right)\) làm một vectơ chỉ phương nên phương trình tham số của đường thẳng AB là:
\(\left\{ \begin{array}{l}x = 3,5\\y = - 2 + 7,5t\\z = 0,4 - 0,4t\end{array} \right.\) (t là tham số).
b) Mặt phẳng (Oxy) có một vectơ pháp tuyến là \(\overrightarrow k = \left( {0;0;1} \right)\).
Do đó, \(\sin \left( {AB,\left( {Oxy} \right)} \right) = \frac{{\left| {0.0 + 7,5.0 + \left( { - 0,4} \right).1} \right|}}{{\sqrt {{0^2} + {{\left( { - 7,5} \right)}^2} + {{\left( { - 0,4} \right)}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{4\sqrt {5641} }}{{5641}}\) nên \(\left( {AB,\left( {Oxy} \right)} \right) \approx {3^o}\). Do đó, góc trượt nằm trong phạm vi cho phép.
c) Mặt phẳng \(\left( \alpha \right)\) là mặt phẳng (MNP).
Ta có: \(\overrightarrow {MN} = \left( { - 5; - 5;0} \right),\overrightarrow {MP} = \left( { - 5;0;0,5} \right)\)
Ta có: \(\left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 5}&0\\0&{0,5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - 5}\\{0,5}&{ - 5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 5}&{ - 5}\\{ - 5}&0\end{array}} \right|} \right) = \left( { - 2,5;2,5; - 25} \right)\)
Mặt phẳng (MNP) nhận \(\left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( { - 2,5;2,5; - 25} \right)\) làm một vectơ pháp tuyến.
Do đó, phương trình mặt phẳng \(\left( \alpha \right)\) là:
\( - 2,5\left( {x - 5} \right) + 2,5\left( {y - 0} \right) - 25\left( {z - 0} \right) \Leftrightarrow x - y + 10z - 5 = 0\)
Vì C là vị trí mà máy bay xuyên qua đám mấy để hạ cánh nên C là giao điểm của đường thẳng AB và mặt phẳng \(\left( \alpha \right)\).
Vì C thuộc AB nên \(C\left( {3,5; - 2 + 7,5t;0,4 - 0,4t} \right)\). Mà C thuộc mặt phẳng \(\left( \alpha \right)\) nên:
\(3,5 - \left( { - 2 + 7,5t} \right) + 10\left( {0,4 - 0,4t} \right) - 5 = 0\), suy ra \(t = \frac{9}{{23}}\). Do đó, \(C\left( {\frac{7}{2};\frac{{43}}{{46}};\frac{{28}}{{115}}} \right)\).
d) Vì D thuộc AB nên \(D\left( {3,5; - 2 + 7,5t';0,4 - 0,4t'} \right)\)
D là vị trí mà máy bay ở độ cao 120m, tức là khoảng cách từ D đến mặt phẳng (Oxy) bằng 120m và bằng 0,12km.
Ta có: \(d\left( {D,\left( {Oxy} \right)} \right) = \frac{{\left| {0,4 - 0,4t'} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = \left| {0,4 - 0,4t'} \right|\)
Do đó, \(\left| {0,4 - 0,4t'} \right| = 0,12 \Leftrightarrow \left[ \begin{array}{l}0,4 - 0,4t' = 0,12\\0,4 - 0,4t' = - 0,12\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t' = 0,7\\t' = 1,3\end{array} \right.\)
Với \(t' = 0,7\) ta có \(D\left( {3,5;3,25;0,12} \right)\).
Với \(t' = 1,3\) ta có \(D\left( {3,5;7,75; - 0,12} \right)\).
Vì D là vị trí độ cao của máy bay nên \(D\left( {3,5;3,25;0,12} \right)\).
e) Ta có: \(DE = \sqrt {{{\left( {3,5 - 3,5} \right)}^2} + {{\left( {4,5 - 3,25} \right)}^2} + {{\left( {0 - 0,12} \right)}^2}} \approx 1,256\left( {km} \right)\)
Vì tầm nhìn xa của phi công sau khi ra khỏi đám mây là \(900m = 0,9km < 1,256km\) nên người phi công đó không đạt được quy định an toàn bay.
Bài tập 11 trang 80 SGK Toán 12 tập 2 thuộc chương trình Cánh diều, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của đại lượng. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài tập 11 thường có dạng như sau: Một vật thể chuyển động theo một quỹ đạo được mô tả bởi một hàm số. Yêu cầu là tìm vận tốc và gia tốc của vật thể tại một thời điểm nhất định, hoặc xác định thời điểm vật thể đạt vận tốc cực đại hoặc cực tiểu.
Bài toán: Một vật thể chuyển động theo hàm số vị trí s(t) = t3 - 6t2 + 9t + 2 (trong đó s tính bằng mét và t tính bằng giây). Tìm vận tốc và gia tốc của vật thể tại thời điểm t = 2 giây.
Giải:
Kết luận: Tại thời điểm t = 2 giây, vận tốc của vật thể là -3 m/s và gia tốc là 0 m/s2.
Ngoài dạng bài tập tìm vận tốc và gia tốc, bài tập 11 trang 80 SGK Toán 12 tập 2 - Cánh diều còn có thể xuất hiện các dạng bài tập khác như:
Để giải quyết các dạng bài tập này, bạn cần nắm vững các kiến thức về đạo hàm, cực trị, và khoảng đơn điệu của hàm số. Ngoài ra, việc vẽ đồ thị hàm số vận tốc và gia tốc có thể giúp bạn hiểu rõ hơn về chuyển động của vật thể.
Ngoài SGK Toán 12 tập 2 - Cánh diều, bạn có thể tham khảo thêm các tài liệu sau để học tập và luyện tập:
Bài tập 11 trang 80 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng rằng với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn khi giải quyết các bài tập tương tự.